Lesson 3: Measurements in Chemistry

Part b: Significant Digits

Part 3a: Precision and Uncertainty
Part 3b: Significant Digits
Part 3c: Evaluating Results

Precision and Significant Digits

We learned on the previous part of Lesson 3 that a measurement includes information about the degree of precision to which the measured quantity is reliably known. This is reflected by the number of digits in the reported value. We refer to these digits as significant digits. Success in a quantitative lab science like Chemistry requires an understanding of measurement. Significant digits is part of that understanding.
 
The precision of a measurement is determined by the number of markings on the instrument used to measure the quantity. The diagram at the right shows the length of a caterpillar being measured with three different centimeter rulers. The three rulers have different spacings between markings. The reported length measurements are given. Each measurement consists of certain numbers and one estimated digit. You will note that as the number of markings increases and the spacing between markings decreases, the level of precision increases. There are more digits in the reported value for the more precise measuring tool.
 
 

All About Zeroes

When it comes to significant digits and measurement, the greatest confusion surrounds the topic of zeroes (0s). We distinguish between three different types of zeroes. There are leading zeroes, captive zeroes, and trailing zeroes. Leading zeroes are located at the beginning of a number in front of non-zero digits. Captive zeroes are located between two non-zero digits. Trailing zeroes are located at the end of numbers after all the non-zero digits. Examples of the three types of zeroes are shown in the three numbers at the right.
 
 
 

Rules for Significant Digits

Measured values are often used in calculations of other quantities. As an example, you might measure a speed and use it to calculate a kinetic energy value. Performing a calculation from a measured quantity should not increase the precision with which you know the value of that measured quantity. If the speed is known to two digits and the kinetic energy depends on speed, it would not make sense to know the kinetic energy with a precision of 12 digits. The level of precision of the calculated quantity cannot be greater the level of precision of the values used to calculate it. For this reason, a Chemistry student will need to be able to count the number of significant digits in a number. We will learn that here. And in Lesson 4 of this Chapter, we will learn how to determine the level of precision in a calculated quantity.
 
 
Like it or not, life works best when you play by the rules. Chemistry class also works best when you play by its rules. Here are the rules for determining the number of significant digits in a number.

1. All non-zero digits in a number are counted as significant digits.
2. Zeroes may or may not be significant. Here’s how to tell:
   1. Leading zeroes are never significant. They are simply placeholders.
   2. Captive zeroes are always significant.
   3. Trailing zeroes are significant if the number contains a decimal point. If there is no decimal point, then a trailing zero serves the role of a placeholder and is not significant.

Examples - Counting Significant Digits

 

Need practice? Check out the Before You Leave and the Check Your Understanding sections below.
 
 
 

Significant Digits and Scientific Notation

The use of scientific notation to express the value of large and small numbers was discussed in Lesson 2. Scientific notation represents a number in the format.

C x 10ⁿ

where C is a number between 1 and 10 and n is a positive or negative integer.
 
When a number is written in scientific notation, the rules for significant digits apply to the C part of the number. Changing a number from standard decimal notation to scientific notation should not change the level of precision. That is, if there are 5 significant digits expressed by standard decimal notation, then there should be 5 significant digits when using scientific notation. Here are a few examples:
 

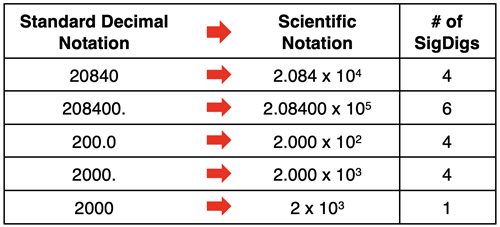
Significant Digits and Calculations

As mentioned above, the reason for the need to count significant digits pertains to the connection between measured values and calculated values. When calculating quantities from measured quantities, it is important to preserve the information about the level of precision. This level of precision is reflected by the number of significant digits. A typical scientific calculator is ignorant of such rules. You will need to be wiser amd sharper than your calculator when it comes to significant digits. We will have more to say about this in Lesson 4.
 
 
 

Before You Leave

1. Download our Study Card on Significant Digits. Save it to a safe location and use it as a review tool. 
2. We have an awesome set of questions in the Units and Measurement Chapter of our Calculator Pad section. Try Problem Set UM1, titled Measurement. And Bonus: you'll get some review of other topics presented in Lessons 1 and 2.
3. Consider some practice - try the first and second activities of our Significant Digits and Measurement Concept Builder; it's titled Measurement.