Waves, Sound and Light: Light Waves
Calculator Pad, Version 2
You are viewing the Legacy Version of The Calculator Pad. We have recently revised and improved The Calculator Pad.
Version 2 is now LIVE! We have more than tripled the number of problems, broken each unit into several smaller, single-topic problem sets, and utilized a random number generator to provide numerical information for each problem. Student answers are automatically evaluated and feedback is instant. And we've maintained the same commitment to providing help via links to existing resources. While the FREE version does all the above, teachers with a Task Tracker subscription can take things a step further. They can modify our pre-made problem sets, write their own problems with our easy-to-use Problem Builder, and use the Calculator Pad to design their own program that expresses their emphasis on the use of mathematics in Physics.
Return to the
Main Page to link into Version 2. Learn more
About Version 2. Or visit the
Store to make a Task Tracker purchase.
Light Waves: Problem Set
Problem 1:
In 1957, the U.S. Naval Research Laboratory conducted the first ever radar measurements of the distance from the Earth to the moon. By reflecting light from an Earth-based source off the moon and measuring the back-and-forth time of transit, scientists determined that the moon is approximately 3.84 x108 m from the Earth. Determine the time it takes light to travel from Earth to the moon and back.
Problem 2:
The distance from the Earth to the sun is 1.496x1011 m. A solar flare occurs on the sun’s surface on Wednesday morning at 10:24 AM. At what time and on what day will electromagnetic radiation from the flare reach the Earth.
Problem 3:
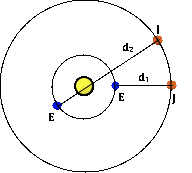 In the 1600s, Ole Roemer became one of the first scientists to make a measurement of the speed of light. Roemer observed the orbits of Jupiter’s nearest moon and recognized that its orbital period was observed to be approximately 22 minutes longer when measured from Earth when it was furthest from Jupiter compared to when it was closest to Jupiter. Roemer reasoned that the difference was due to the fact that it took longer for light from Jupiter to travel the extra distance when Earth’s position was on the opposite side of the Sun from Jupiter. The distance d2 is 2.98x1011 m greater than the distance d1. Determine Roemer’s estimate of the speed of light in the 1600s.
In the 1600s, Ole Roemer became one of the first scientists to make a measurement of the speed of light. Roemer observed the orbits of Jupiter’s nearest moon and recognized that its orbital period was observed to be approximately 22 minutes longer when measured from Earth when it was furthest from Jupiter compared to when it was closest to Jupiter. Roemer reasoned that the difference was due to the fact that it took longer for light from Jupiter to travel the extra distance when Earth’s position was on the opposite side of the Sun from Jupiter. The distance d2 is 2.98x1011 m greater than the distance d1. Determine Roemer’s estimate of the speed of light in the 1600s.
Problem 4:
The German-born, American physicist Albert Michelson devoted much of his life to the accurate measurement of the speed of light. In 1923, he positioned mirrors and detectors on two different California mountains positioned nearly 35 km (nearly 22 miles) apart. Using a sophisticated timing method of involving the rotating of octagonal mirrors, Michelson determined the speed of light to be 299,774 km/sec. At this speed, estimate the time it takes light to travel 35 km between mountains.
Problem 5:
Mr. H catches the news on 780 AM, which broadcasts at 780. kHz. Determine the wavelength of these radio waves.
Problem 6:
Determine the frequency of … (GIVEN: 1 m = 109 nm)
a. … red visible light (λ = 650 nm)
b. … violet visible light (λ = 420 nm)
Problem 7:
Determine the wavelength of the microwave radiation emitted …
a. … by a microwave oven (f = 2.45x109 Hz).
b. … by a cordless phone (f = 5.8x109 Hz).
Problem 8:
Determine the wavelength of the infrared carrier wave transmitted by a television remote control at 38 kHz.
Problem 9:
a. Determine the frequency of electromagnetic radiation which would have a wavelength of 1.0 mile (1.6 km).
b. What part of the electromagnetic spectrum does this fall within?
Problem 10:
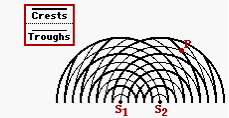 Like light waves, water waves emerging from two sources interferes in the space surrounding the sources to produce a pattern of nodes and antinodes lying along lines. The diagram at the right represents the interference pattern created by two water waves. The waves were created by two objects bobbing up and down in phase at the same frequency. Point P on the pattern is a distance of 34.0 cm from S1 and 23.8 cm from S2. Determine the wavelength (in cm) of the water waves.
Like light waves, water waves emerging from two sources interferes in the space surrounding the sources to produce a pattern of nodes and antinodes lying along lines. The diagram at the right represents the interference pattern created by two water waves. The waves were created by two objects bobbing up and down in phase at the same frequency. Point P on the pattern is a distance of 34.0 cm from S1 and 23.8 cm from S2. Determine the wavelength (in cm) of the water waves.
Problem 11:
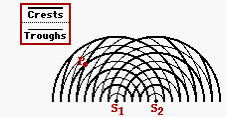 The diagram at the right represents the interference pattern created by two water waves. The waves were created by two objects bobbing up and down in phase at the same frequency. Point P on the pattern is a distance of 36.9 cm from S1 and 61.5 cm from S2. Determine the wavelength (in cm) of the water waves.
The diagram at the right represents the interference pattern created by two water waves. The waves were created by two objects bobbing up and down in phase at the same frequency. Point P on the pattern is a distance of 36.9 cm from S1 and 61.5 cm from S2. Determine the wavelength (in cm) of the water waves.
Problem 12:
Water waves with a wavelength of 7.8 cm are created in a ripple tank by two in-phase sources bobbing up and down at the same frequency. The waves form an interference pattern in the space surrounding the sources. A point on the fourth nodal line is a distance of 58.2 cm from the nearest source. Determine the distance from this same point to the furthest source.
Problem 13:
Mr. H takes his class to the gymnasium to investigate two point source interference patterns produced by sound waves from two sound sources. The pure-tone output from a frequency generator is split and fed to two audio speakers positioned about 1-meter apart. The sound from the two speakers travels through the gymnasium and interferes constructively and destructively to create a pattern of nodes and antinodes. Mr. H directs the class to stand with one ear facing the speakers and the other ear covered and to walk slowly across the gymnasium, observing positions of relatively soft and loud sounds in alternating fashion. Once initial observations are made, Mr. H asks all the male students to stand at nodal positions and all the female students to stand at antinodal positions. Once done, Mr. H takes a picture of their positions and then makes several measurements of the distances between students and from some selected students to the speakers. Some sample data are shown below. Complete the table, determining the wavelength of the sound waves based on each student’s measurements.
| Student |
Nodal or
Antinodal Line |
Distance to
Speaker 1 (m) |
Distance to
Speaker 2 (m) |
Wavelength (m) |
| Jeremy |
1st Nodal |
14.45 |
13.52 |
|
| Bridget |
1st Antinodal |
21.64 |
23.42 |
|
| Jane |
3rd Antinodal |
16.22 |
21.67 |
|
| Jose |
4th Nodal |
25.22 |
19.10 |
|
Problem 14:
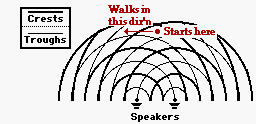 Two audio speakers have been arranged in a large room so as to produce a sound interference pattern. Miguel starts at a position on the central antinodal line and begins to slowly walk parallel to the imaginary line connecting the speakers. Miguel stops at the first position of minimum loudness. At this position, he is a distance of 17.9 m from the nearest speaker. Sound waves travel through the room at 345 m/s and the speakers are sounding out a frequency of 244 Hz.
Two audio speakers have been arranged in a large room so as to produce a sound interference pattern. Miguel starts at a position on the central antinodal line and begins to slowly walk parallel to the imaginary line connecting the speakers. Miguel stops at the first position of minimum loudness. At this position, he is a distance of 17.9 m from the nearest speaker. Sound waves travel through the room at 345 m/s and the speakers are sounding out a frequency of 244 Hz.
a. Determine the wavelength of the sound waves.
b. Determine the distance from Miguel to the furthest speaker.
Problem 15:
Mr. H’s period 7 physics class is attempting to duplicate Thomas Young’s experiment in which they use a two-point source light interference pattern to measure the wavelength of light. They red shine laser light through a slide containing a double slit; the slit spacing is 0.125 mm. The light interference pattern created by the light which passes through the slits is projected on a screen a distance of 10.72 m away. Justin and Shirley measure the distance from the 3rd antinodal bright spots on opposite sides of the pattern to be 33.9 cm apart. Based on these measurements, what is the wavelength of the red laser light.
Problem 16:
Two narrow slits in a slide are separated by a distance of 45.0 micrometers. Light from a green laser (λ = 532 nm) is passed through the slits and the interference pattern is projected onto a screen 9.85 m away. Determine the distance between the central bright spot and the fourth bright spot. (GIVEN: 1 m = 106 mm)
Problem 17:
Jackson and Melanie are doing the Young’s Experiment Lab using a red laser pen and a slide with two slits spaced 25 micrometers apart. They project the interference pattern onto a whiteboard located 2.35 m from the slits. They measure the distance from the 3rd bright band on opposite sides of the pattern to be separated by 37 cm. Based on these measurements, what is the wavelength of the red laser light (in nanometers)? (GIVEN: 1 m = 106 mm, 1 m = 109 nm)
Problem 18:
Maria and Jason are doing the same lab as Jackson and Melanie (from the previous problem). Maria and Jason determine the distance between the central bight spot and the 4th bright spot to be 29 cm. The distance from their slide to the whiteboard (where the interference pattern is projected) is 2.76 m. The slits in their slide are also spaced 25 micrometers apart. Based on Maria and Jason’s measurements, what is the wavelength of the red laser light (in nanometers)? (GIVEN: 1 m = 106 mm, 1 m = 109 nm)
Problem 19:
Jill is helping her younger brother Nathan set up an exhibit for a Science Fair. Nathan’s exhibit pertains to the wave-particle nature of light waves. He wishes to demonstrate the wave nature of light by displaying the two point interference pattern of red laser light (λ = 648 nm). Nathan has purchased a double slit slide from a science warehouse which has slits separated a distance of 0.125 mm. Nathan has asked Jill to determine the slide-to-screen distance which will result in a 2.0 cm separation between adjacent bright spots. What distance will result in this antinodal spacing?
Problem 20:
The Bluebird Library has been celebrating the lives of famous scientists. Each month, a new scientist is selected and displays are created to feature the discoveries and contribution of the scientist. April's scientist of the month is Thomas Young; the library wishes to develop a Young's experient display. The library has purchased a blue laser which emits light with a wavelength of 473 nm. They also have purchased a slide with a double slit; the slit spacing is 44 µm. The library's current plans are to project the interference pattern onto a white board which is 3 feet wide and located 28 feet from the slits. What is the maximum number of bright spots which will appear on the board at these distances and what is the spacing distance between each bright spot? Assume that each bright spot is bright enough to see. (GIVEN: 1 m = 3.28 ft, 1 m = 106 mm, 1 m = 109 nm)
Problem 21:
Monochromatic yellow light (λ = 594 nm) passes throught two slits with a slit spacing of 0.125 mm and forms an interference pattern on a screen that is positioned 14.5 m away. Determine the distance between the fifth bright spots on opposite sides of the central bright spot.
Problem 22:
In a museum exhibit, monochromatic red light (λ = 648 nm) passes through a double slit and is projected onto a screen located 16.8 m from the slits. A metric ruler located above the interference pattern clearly shows the fifth dark fringe to be located 42.0 cm from the central bright spot. Determine the slit separation distance.
Problem 23:
A radio station has two antennae which are used to broadcast their 582 kHz radio wave signal. The Robinson family, who lives in the Cedar Ridge subdivision, have very poor reception when tuned to this signal due to the destructive interference of radio waves from the two antennae. The Robinson home is located a distance of 13.78 km from the nearest antenna. What is the likely minimum distance from the Robinson’s home to the furthest antenna?
Problem 24:
Always thinking ahead, Mr. H is investigating possible retirement communities in Flagstaff, Arizona. His favorite radio station in the Flagstaff area is KFIZ, broadcasting at 1420 kHz. One of the communities Mr. H is investigating is nestled in the cliffs, directly facing the KFIZ broadcasting station located several miles away. While driving through the neighborhood, Mr. H observes the KFIZ signal fading in and out. Mr. H reasons that the cause of the poor reception is that radio waves coming directly from the station undergoing are destructively interfering with waves which reflect off the cliffs from behind the retirement community. Knowing he must consider all factors in the purchase of a home, Mr. H decides to calculate all the possible distances from the cliffs for which destructive interference occurs. By doing so, he will be able to rule out the purchase of several lots in the neighborhood. Determine the six nearest distances from the cliffs that result in destructive interference of the 1420 kHz signal. (Assume that the reflected waves do not undergo a phase change upon reflection off the plane.)
Problem 25:
Noah Formula lives near the airport and frequently notices poor AM radio reception occurring as planes use the approach path which passes over his home. Having just finished the unit on light wave behavior, Noah now understands that the reception problem occurs because of radio wave signals reflecting off the planes and destructively interfering with waves which approach his antenna directly from the station. Noah’s favorite station – WFIZ – broadcasts at 1240 kHz and is located several miles from his home. Determine the five lowest heights above his home for which reflection off of planes will lead to destructive interference of this 1240 kHz signal. (Assume that the reflected waves do not undergo a phase change upon reflection off the plane.)

Return to Overview
View Audio Guided Solution for Problem:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25