Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 Refraction is the bending of the path of a light wave as it passes across the boundary separating two media. Refraction is caused by the change in speed experienced by a wave when it changes medium. In Lesson 1, we learned that if a light wave passes from a medium in which it travels slow (relatively speaking) into a medium in which it travels fast, then the light wave would refract away from the normal. In such a case, the refracted ray will be farther from the normal line than the incident ray; this is the SFA rule of refraction. On the other hand, if a light wave passes from a medium in which it travels fast (relatively speaking) into a medium in which it travels slow, then the light wave will refract towards the normal. In such a case, the refracted ray will be closer to the normal line than the incident ray is; this is the FST rule of refraction. These two rules regarding the refraction of light only indicate the direction that a light ray bends; they do not indicate how much bending occurs. Lesson 1 focused on the topics of "What causes refraction?" and "Which direction does light refract?" Lesson 2 will focus on the question of "By how much does light refract when it crosses a boundary?"
Refraction is the bending of the path of a light wave as it passes across the boundary separating two media. Refraction is caused by the change in speed experienced by a wave when it changes medium. In Lesson 1, we learned that if a light wave passes from a medium in which it travels slow (relatively speaking) into a medium in which it travels fast, then the light wave would refract away from the normal. In such a case, the refracted ray will be farther from the normal line than the incident ray; this is the SFA rule of refraction. On the other hand, if a light wave passes from a medium in which it travels fast (relatively speaking) into a medium in which it travels slow, then the light wave will refract towards the normal. In such a case, the refracted ray will be closer to the normal line than the incident ray is; this is the FST rule of refraction. These two rules regarding the refraction of light only indicate the direction that a light ray bends; they do not indicate how much bending occurs. Lesson 1 focused on the topics of "What causes refraction?" and "Which direction does light refract?" Lesson 2 will focus on the question of "By how much does light refract when it crosses a boundary?"
The question is: "By how much does light refract when it crosses a boundary?" Perhaps there are numerous answers to such a question. (For example, "a lot," "a little," "like wow! Quite a bit dude," 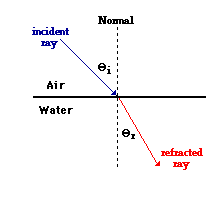 etc.) The concern of this lesson is to express the amount of refraction of a light ray in terms of a measurable quantity that has a mathematical value. The diagram to the right shows a light ray undergoing refraction as it passes from air into water. As mentioned in Lesson 1, the incident ray is a ray (drawn perpendicular to the wavefronts) that shows the direction that light travels as it approaches the boundary. (The meaning of an incident ray was first introduced in the discussion of Reflection of Light in Unit 13 of The Physics Classroom Tutorial.) Similarly, the refracted ray is a ray (drawn perpendicular to the wavefronts) that shows the direction that light travels after it has crossed over the boundary. In the diagram, a normal line is drawn to the surface at the point of incidence. This line is always drawn perpendicular to the boundary. The angle that the incident ray makes with the normal line is referred to as the angle of incidence. Similarly, the angle that the refracted ray makes with the normal line is referred to as the angle of refraction. The angle of incidence and angle of refraction are denoted by the following symbols:
etc.) The concern of this lesson is to express the amount of refraction of a light ray in terms of a measurable quantity that has a mathematical value. The diagram to the right shows a light ray undergoing refraction as it passes from air into water. As mentioned in Lesson 1, the incident ray is a ray (drawn perpendicular to the wavefronts) that shows the direction that light travels as it approaches the boundary. (The meaning of an incident ray was first introduced in the discussion of Reflection of Light in Unit 13 of The Physics Classroom Tutorial.) Similarly, the refracted ray is a ray (drawn perpendicular to the wavefronts) that shows the direction that light travels after it has crossed over the boundary. In the diagram, a normal line is drawn to the surface at the point of incidence. This line is always drawn perpendicular to the boundary. The angle that the incident ray makes with the normal line is referred to as the angle of incidence. Similarly, the angle that the refracted ray makes with the normal line is referred to as the angle of refraction. The angle of incidence and angle of refraction are denoted by the following symbols:
|
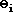
|
= angle of incidence
|
|
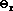
|
= angle of refraction
|
The Amount of Bending
The amount of bending that a light ray experiences can be expressed in terms of the angle of refraction (more accurately, by the difference between the angle of refraction and the angle of incidence). A ray of light may approach the boundary at an angle of incidence of 45-degrees and bend towards the normal. If the medium into which it enters causes a small amount of refraction, then the angle of refraction might be a value of about 42-degrees. On the other hand if the medium into which the light enters causes a large amount of refraction, the angle of refraction might be 22-degrees. (These values are merely arbitrarily chosen values to illustrate a point.) The diagram below depicts a ray of light approaching three different boundaries at an angle of incidence of 45-degrees. The refractive medium is different in each case, causing different amounts of refraction. The angles of refraction are shown on the diagram.
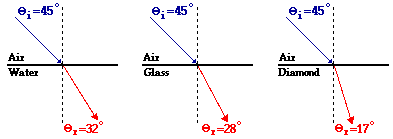
Of the three boundaries in the diagram, the light ray refracts the most at the air-diamond boundary. This is evident by the fact that the difference between the angle of incidence and the angle of refraction is greatest for the air-diamond boundary. But how can this be explained? The cause of refraction is a change in light speed; and wherever the light speed changes most, the refraction is greatest. We have already learned that the speed is related to the optical density of a material that is related to the index of refraction of a material. Of the four materials present in the above diagram, air is the least dense material (lowest index of refraction value) and diamond is the most dense material (largest index of refraction value). Thus, it would be reasonable that the most refraction occurs for the transmission of light across an air-diamond boundary.
In this example, the angle of refraction is the measurable quantity that indicates the amount of refraction taking place at any boundary. A comparison of the angle of refraction to the angle of incidence provides a good measure of the refractive ability of any given boundary. For any given angle of incidence, the angle of refraction is dependent upon the speeds of light in each of the two materials. The speed is in turn dependent upon the optical density and the index of refraction values of the two materials. There is a mathematical equation relating the angles that the light rays make with the normal to the indices (plural for index) of refraction of the two materials on each side of the boundary. This mathematical equation is known as Snell's Law and is the topic of the next section of Lesson 2.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Refraction Interactive. You can find it in the Physics Interactives section of our website. The
Refraction Interactive provides the learner an interactive enivronment for exploring the refraction and reflection of light at a boundary between two materials.