Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Earlier in Lesson 6, we learned that the eye consists of a cornea (thin outer membrane), a lens attached to 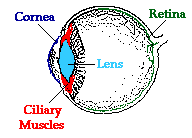 ciliary muscles, and a retina (inner surface equipped with nerve cells). These four parts of the eye are the most instrumental in the task of producing images that are discernible by the brain. In order to facilitate the ability to see, each part must enable the eye to refract light so that is produces a focused image on the retina.
ciliary muscles, and a retina (inner surface equipped with nerve cells). These four parts of the eye are the most instrumental in the task of producing images that are discernible by the brain. In order to facilitate the ability to see, each part must enable the eye to refract light so that is produces a focused image on the retina.
It is a surprise to most people to find out that the lens of the eye is not where all the refraction of incoming light rays takes place. Most of the refraction occurs at the cornea. The cornea is the outer membrane of the eyeball that has an index of refraction of 1.38. The index of refraction of the cornea is significantly greater than the index of refraction of the surrounding air. This difference in optical density between the air the corneal material combined with the fact that the cornea has the shape of a converging lens is what explains the ability of the cornea to do most of the refracting of incoming light rays. The crystalline lens is able to alter its shape due to the action of the ciliary muscles. This serves to induce small alterations in the amount of corneal bulge as well as to fine-tune some of the additional refraction that occurs as light passes through the lens material.
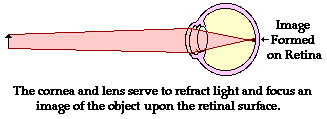
The bulging shape of the cornea causes it to refract light in a manner to similar to a double convex lens. The focal length of the cornea-lens system varies with the amount of contraction (or relaxation) of the ciliary muscles and the resulting shape of the lens. In general, the focal length is approximately 1.8 cm, give or take a millimeter. As learned in our discussion of convex lenses in Lesson 5, the image location, size, orientation, and type is dependent upon the location of the object relative to the focal point and the 2F point of a lens system. Since the object is typically located at a point in space more than 2-focal lengths from the "lens," the image will be located somewhere between the focal point of the "lens" and the 2F point. The image will be inverted, reduced in size, and real. Quite conveniently, the cornea-lens system produces an image of an object on the retinal surface. The process by which this occurs is known as accommodation and will be discussed in more detail in the next part of Lesson 6. Fortunately, the image is a real image - formed by the actual convergence of light rays at a point in space. Vision is dependent upon the stimulation of nerve impulses by an incoming light rays. Only real images would be capable of producing such a stimulation. Finally, the reduction in the size of the image allows the entire image to "fit" on the retina. The fact that the image is inverted poses no problem. Our brain has become quite accustomed to this and properly interprets the signal as originating from a right-side-up object.
Quantitative Relationships Between do, di and f
The use of the lens equation and magnification equation can provide an idea of the quantitative relationship between the object distance, image distance and focal length. For now we will assume that the cornea-lens system has a focal length of 1.80 cm (0.0180 m). We will attempt to determine the image size and image location of a 6-foot tall man (ho=1.83 m) who is standing a distance of approximately 10 feet away (do= 3.05 meters). (The lens equation is derived geometrically upon the assumption that the lens is a thin lens. The lens of the eye is anything but thin and as such the lens equation does not provide a truly accurate model of the eye lens. Despite this fact, we will use the equation as a simplified approximation of the mathematics of the eye.)
Like all problems in physics, begin by the identification of the known information.
|
do = 3.05 m
|
ho = 1.83 m
|
f = 0.0180 m
|
Next identify the unknown quantities that you wish to solve for.
To determine the image distance, the lens equation can be used. The following lines represent the solution to the image distance; substitutions and algebraic steps are shown.
1/f = 1/do + 1/di
1/(0.0180 m) = 1/(3.05 m) + 1/di
55.6 m-1 = 0.328 m-1 + 1/di
55.2 m-1 = 1/di
To determine the image height, the magnification equation is needed. Since three of the four quantities in the equation (disregarding the M) are known, the fourth quantity can be calculated. The solution is shown below.
hi/ho = - di/do
hi /(1.83 m) = - ( 0.0181 m)/(3.05 m)
hi = - (1.83 m) • (0.0181m)/(3.05 m)
|
hi = -0.0109 m = -1.09 cm
|
From the calculations in this problem it can be concluded that if a 1.83-m tall person is standing 3.05 m from your cornea-lens system having a focal length of 1.8 cm, then the image will be inverted, 1.09-cm tall (the negative values for image height indicate that the image is an inverted image) and located 1.81 cm from the "lens".
Now of course, if the person is standing further away (or closer to) the eye, the image size and image distance will be adjusted accordingly. This is illustrated in the following table for the same 6-foot tall (1.83 m) person.
Dependence of himage and dimage on dobject
(focal length is fixed at 1.8 cm)
|
Object Distance
|
Image Distance
|
Image Height
|
|
1.00 m
|
1.83 cm
|
3.35 cm
|
|
3.05 m
|
1.81 cm
|
1.09 cm
|
|
100 m
|
1.80 cm
|
0.329 cm
|
|
Interpreting the Results
The results of these calculations (as illustrated in the table above) illustrate two important principles concerning the ability of the eye to discern objects that are both close up and far away. First, the distance between the observer and the object will greatly influence the image size (height and width of the image formed on the retina) and quality. Objects that are viewed at close proximity produce images that are larger than distant objects. Such an image is typically spread over the entirety of the retina and even at times would extend beyond the extremities of the retina. Thus, the full dimensions of a 6-foot tall person cannot be seen if he/she stands 1-meter away (unless the eyeballs are rolled in their socket). On the other hand, the entire image of the same person can easily be seen when standing 100-meters away. In this instance, the image takes up a small amount of space on the back of the retina. The drawback however is that the finer details of the image are lost due to the reduction in the size of the image. Since the image is stimulating a smaller region of nerve cells, some details are lost since they fail to provide sufficient stimulation to allow the brain to discern them. For such an object distance, the small image that is created of a man might make it impossible to discern that the man's fly is open or that his socks and belt don't match.
Second, the varying distance between the observer and the object poses some potential problems for the human eye. Objects located varying distances from a lens system with a fixed focal length produce images that are varying distances from the lens. Yet, the eye must always produce an image on the retina - a location that is always the same distance away from the cornea. The eye cannot afford to allow changes in the image distance. So how does an eye always focus images with the same dimage regardless of the fact that the dobject is different? How can an object 100 meters away be focused the same distance from the cornea-lens system as an object that is 1 meter away? The answer: the cornea-lens system is able to change its focal length. The ciliary muscles of the eye serve to contract and relax, thus changing the shape of the lens. This serves to allow the eye to change its focal length and thus appropriately focus images of objects that are both close up and far away. This process is known as accommodation and is the focus of the next part of Lesson 6.