Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 As mentioned earlier, all objects have a frequency or set of frequencies with which they naturally vibrate when struck, plucked, strummed or somehow disturbed. Each of the natural frequencies at which an object vibrates is associated with a standing wave pattern. When an object is forced into resonance vibrations at one of its natural frequencies, it vibrates in a manner such that a standing wave is formed within the object. The topic of standing wave patterns was introduced in Unit 10 of The Physics Classroom. In that unit, a standing wave pattern was described as a vibrational pattern created within a medium when the vibrational frequency of a source causes reflected waves from one end of the medium to interfere with incident waves from the source. The result of the interference is that specific points along the medium appear to be standing still while other points vibrated back and forth. Such patterns are only created within the medium at specific frequencies of vibration. These frequencies are known as harmonic frequencies or merely harmonics. At any frequency other than a harmonic frequency, the interference of reflected and incident waves results in a disturbance of the medium that is irregular and non-repeating.
As mentioned earlier, all objects have a frequency or set of frequencies with which they naturally vibrate when struck, plucked, strummed or somehow disturbed. Each of the natural frequencies at which an object vibrates is associated with a standing wave pattern. When an object is forced into resonance vibrations at one of its natural frequencies, it vibrates in a manner such that a standing wave is formed within the object. The topic of standing wave patterns was introduced in Unit 10 of The Physics Classroom. In that unit, a standing wave pattern was described as a vibrational pattern created within a medium when the vibrational frequency of a source causes reflected waves from one end of the medium to interfere with incident waves from the source. The result of the interference is that specific points along the medium appear to be standing still while other points vibrated back and forth. Such patterns are only created within the medium at specific frequencies of vibration. These frequencies are known as harmonic frequencies or merely harmonics. At any frequency other than a harmonic frequency, the interference of reflected and incident waves results in a disturbance of the medium that is irregular and non-repeating.
Natural Frequencies and Vibrational Patterns
So the natural frequencies of an object are merely the harmonic frequencies at which standing wave patterns are established within the object. These standing wave patterns represent the lowest energy vibrational modes of the object. While there are countless ways by which an object can vibrate (each associated with a specific frequency), objects favor only a few specific modes or patterns of vibrating. The favored modes (patterns) of vibration are those that result in the highest amplitude vibrations with the least input of energy. Objects favor these natural modes of vibration because they are representative of the patterns that require the least amount of energy. Objects are most easily forced into resonance vibrations when disturbed at frequencies associated with these natural frequencies.
The wave pattern associated with the natural frequencies of an object is characterized by points that appear to be standing still. For this reason, the pattern is often called a "standing wave pattern." The points in the pattern that are standing still are referred to as nodal points or nodal positions. These positions occur as the result of the destructive interference of incident and reflected waves. Each nodal point is surrounded by antinodal points, creating an alternating pattern of nodal and antinodal points. Such patterns were introduced in Unit 10 of The Physics Classroom Tutorial. In this unit, we will elaborate on the essential characteristics and the causes of standing wave patterns and relate these patterns to the vibrations of musical instruments.
Chladni Plates
A common Physics demonstration utilizes a square metal plate (known as a Chladni plate), a violin bow and salt. The plate is securely fastened to a table using a nut and bolt. The nut and bolt  are clamped to the center of the square plate, preventing that section from vibrating. Salt (or sand) is sprinkled upon the plate in an irregular pattern. Then the violin bow is used to induce vibrations within the plate; the plate is strummed and begins vibrating. And then the magic occurs. A high-pitched pure tone is sounded out as the plate vibrates. And, remarkably (as is often the case in a physics class), the salt upon the plate begins vibrating and forms a pattern upon the plate. As we know, all objects (even a silly little metal plate) have a set of natural frequencies at which they vibrate; and each frequency is associated with a standing wave pattern. The pattern formed by the salt on the plate is the standing wave pattern associated with one of the natural frequencies of the Chladni plate. As the plate vibrates, the salt begins to vibrate and tumble about the plate until it reaches points along the plate that are not vibrating. Subsequently, the salt finally comes to rest along the nodal positions. The diagrams at the right show two of the most common standing wave patterns for the Chladni plates. The white lines represent the salt locations (nodal positions). Observe in the diagram that each pattern is characterized by nodal positions in the corners of the square plate and in the center of the plate. For these two particular vibrational modes, those positions are unable to move. Being unable to move, they become nodal points - points of no displacement.
are clamped to the center of the square plate, preventing that section from vibrating. Salt (or sand) is sprinkled upon the plate in an irregular pattern. Then the violin bow is used to induce vibrations within the plate; the plate is strummed and begins vibrating. And then the magic occurs. A high-pitched pure tone is sounded out as the plate vibrates. And, remarkably (as is often the case in a physics class), the salt upon the plate begins vibrating and forms a pattern upon the plate. As we know, all objects (even a silly little metal plate) have a set of natural frequencies at which they vibrate; and each frequency is associated with a standing wave pattern. The pattern formed by the salt on the plate is the standing wave pattern associated with one of the natural frequencies of the Chladni plate. As the plate vibrates, the salt begins to vibrate and tumble about the plate until it reaches points along the plate that are not vibrating. Subsequently, the salt finally comes to rest along the nodal positions. The diagrams at the right show two of the most common standing wave patterns for the Chladni plates. The white lines represent the salt locations (nodal positions). Observe in the diagram that each pattern is characterized by nodal positions in the corners of the square plate and in the center of the plate. For these two particular vibrational modes, those positions are unable to move. Being unable to move, they become nodal points - points of no displacement.

Flickr Physics Photo
Salt is sprinkled onto a metal plate. The plate is strummed with a violin bow and set into vibration. The salt crystals vibrate about the plate until they settle onto positions of nodes (points of no despacement). Several patterns can be obtained, each associated with a unique frequency of vibrations. These standing wave patterns are known as Chladni patterns, named in honor of a 19th century German physicist who advanced our understanding of acoustics and the physics of music.

Standing Wave Patterns for Vibrating Strings
The diagram below depicts one of the natural patterns of vibrations for a guitar string. In the pattern, you will note that there are certain positions along the string (the medium) that appear to be standing still. These positions are referred to as nodes and are labeled on the diagram. In between each nodal position, there are other positions that appear to be vibrating back and forth between a large upward displacement to a large downward displacement. These points are referred to as antinodes and are also labeled on the diagram. There is an alternating pattern of nodal and antinodal positions in a standing wave pattern.
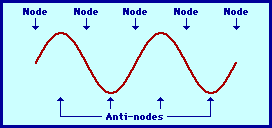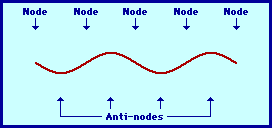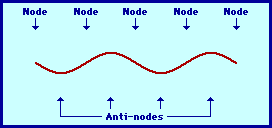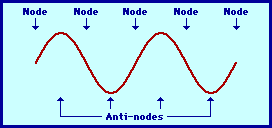
Because the antinodal positions along the guitar string are vibrating back and forth from a large upward displacement to a large downward displacement, the standing wave pattern is often depicted by a diagram such as that shown below.
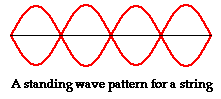
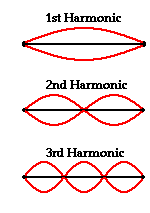 The pattern above is not the only pattern of vibration for a guitar string. There are a variety of patterns by which the guitar string could naturally vibrate. Each pattern is associated with one of the natural frequencies of the guitar strings. Three other patterns are shown in the diagrams at the right. Each standing wave pattern is referred to as a harmonic of the instrument (in this case, the guitar string). The three diagrams at the right represent the standing wave patterns for the first, second, and third harmonics of a guitar string. (Harmonics will be discussed in more detail in the next section of this lesson.)
The pattern above is not the only pattern of vibration for a guitar string. There are a variety of patterns by which the guitar string could naturally vibrate. Each pattern is associated with one of the natural frequencies of the guitar strings. Three other patterns are shown in the diagrams at the right. Each standing wave pattern is referred to as a harmonic of the instrument (in this case, the guitar string). The three diagrams at the right represent the standing wave patterns for the first, second, and third harmonics of a guitar string. (Harmonics will be discussed in more detail in the next section of this lesson.)
There are a variety of other low energy vibrational patterns that could be established in the string. For guitar strings, each pattern is characterized by some basic traits:
- There is an alternating pattern of nodes and antinodes.
- There are either a half-number or a whole number of waves within the pattern established on the string.
- Nodal positions (points of no displacement) are established at the ends of the string where the string is clamped down in a fixed position.
- One pattern is related to the next pattern by the addition (or subtraction) of one or more nodes (and antinodes).
The standing wave patterns for other musical instruments share some of these same or at least similar traits. These patterns will be discussed in more detail in Lesson 5 of this unit.
|
1st Harmonic
|
2nd Harmonic
|
3rd Harmonic
|

|

|

|
Watch It!
A physics instructor demonstrates and explains the formation of a longitudinal standing wave in a spring.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Standing Wave Patterns Interactive. You can find it in the Physics Interactives section of our website. The
Standing Wave Patterns Interactive provides the learner an environment for exploring the formation of standing waves, standing wave patterns, and mathematical relationships for standing wave patterns.