The Physics Classroom » Chemistry Tutorial » The Modern Atomic Model » Quantum Numbers

Lesson 2: The Quantum Mechanical Model

Part d: Quantum Numbers

Part 2a: Schrodinger's Wave Mechanical Model
Part 2b: Orbitals
Part 2c: Energy Levels
Part 2d: Quantum Numbers

 

Importance of Quantum Numbers

The Wave Mechanical Model or Quantum Mechanical Model is a complex mathematical description of the atom and its electrons. The model relies on the use of a wave function to describe the properties and behaviors of an electron inside an atom. Valid solutions to the wave function yield a unique set of four numerical values to describe an electron and the region of space in which it is located. These numerical values are referred to as quantum numbers. The quantum numbers describe the regions of space where we might find an electron, the energy of the electron, and the direction that the electron spins. Each quantum number has a name and a set of restrictions which govern the allowed numerical values that an electron can have.
 
Thus far in Lesson 2, we have only described the bare requirements that one must know regarding quantum numbers in order to understand the atomic orbitals of an atom. In Part d of Lesson 2 we will describe more details regarding the four quantum numbers, providing greater insight into the beauty and complexity of quantum mechanics. This page is for those who need to know more (due to course requirements) or are simply curious about the intricacies of quantum mechanics.
 
 
 
Principal Quantum Number
The first quantum number is referred to as the principal quantum number and is represented by the symbol n. It is a positive, integer with allowed values of 1, 2, 3, etc. The n value describes the principal energy level of the electron. It also describes the size of the region of space that the electron is located in. Larger n values indicate greater principal energy levels and larger regions of space. These regions of space, sometimes described as electron shells, are composed of atomic orbitals. The atomic orbitals hold electrons. The number of atomic orbitals present in any electron shell is the square of the n value (n2) for that electron shell. The n=1 electron shell consists of only one (12) orbital. The n=2 electron shell consists of four (22) orbitals. The n=3 electron shell consists of only nine (32) orbitals. Since a maximum of two electrons can fit in each orbital, the number of electrons in any given electron shell or energy level is 2•n2. There are a variety of types of orbitals, each distinguished from one another by a unique shape. The number of types of orbitals in each electron shell is equal to the n value of the electron shell. There is one type of orbital in the n=1 electron shell, two types of orbitals in the n=2 electron shell, three types of orbitals in the n=3 electron shell, etc.
 

 

 
 

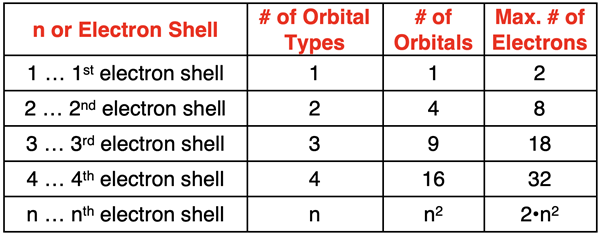
Azimuthal Quantum Number

The second quantum number is referred to as the azimuthal quantum number and is represented by the symbol l. The number of allowed values of l depends on and is equal to the value of the principal quantum number (n). The first electron shell (n=1) allows 1 value of l. The second electron shell (n=2) allows 2 values of l. The allowed values of l start at 0 and increment by 1 up to the n-1. So, if n=4, allowed values of l are 0, 1, 2, and 3.
 
The azimuthal quantum number describes the shape of an orbital that houses an electron. An l value of 0 corresponds to a spherical shaped orbital known as the s orbital. An l value of 1 corresponds to a dumbbell shaped orbital known as the p orbital. The d orbitals are represented by l values of 2 and f orbitals are represented by l values of 3.
 
The number of orbitals of each type is equal to 2•l + 1. For any given electron shell, an l value of 1 indicates that there are 3 (from 2•1+1) p orbitals. An l value of 2 indicates that there are 5 (from 2•2+1) d orbitals. And an l value of 3 indicates that there are 7 (from 2•3+1) f orbitals.

 
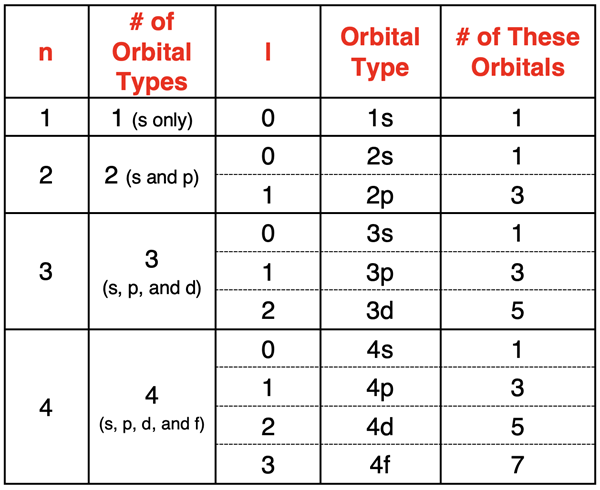
The azimuthal quantum number (l) also determines the energy sublevel of the electron. Each orbital type has a different energy than other orbital types in the same electron shell. For the same n value, the energy sublevel increases with increasing l value. For instance, the 3d orbitals (n=3, l=2) are higher in energy than the 3s orbitals (n=3, l=0).
 

 

In Case Your Curious

There are also g and h orbitals. As of this writing (2024), there are 118 known elements. The greatest number of electrons in an atom is 118. There will likely be more elements discovered. According to quantum mechanics, the 119th and 120th electrons will be in 8s orbitals. The 121st electron will enter the lowest energy g orbital – a 5g orbital. Stay grounded, because it might be a few years still before we need those g orbitals … unless something gets rather excited (like an electron).


 
 

Magnetic Quantum Number

The third quantum number is referred to as the magnetic quantum number and is represented by the symbol ml. The number of allowed values of ml depends on the value of l and is equal to 2•l + 1. The allowed values of ml are the integers ranging from -l to +l. For instance, if l=2 (signifying d orbitals), ml has values of {-2,-1,0,+1,+2}. And if l=3 (signifying f orbitals), ml has values of {-3,-2,-1,0,+1,+2,+3}.
 
As you can see, each individual orbital of an energy sublevel has its own unique ml value. We often say that the ml value determines the spatial orientation of the orbitals. For instance, the 2p orbitals are considered the l=1 sublevel of the n=2 principal energy level. There are three different 2p orbitals, each with a different spatial orientation. One aligned with lobes along the x-axis, one with lobes aligned along the y-axis, and one with lobes aligned along the z axis. There are three different ml values for these p orbitals, one for each spatial orientation relative to the x-y-z axes.
 

 
 
 

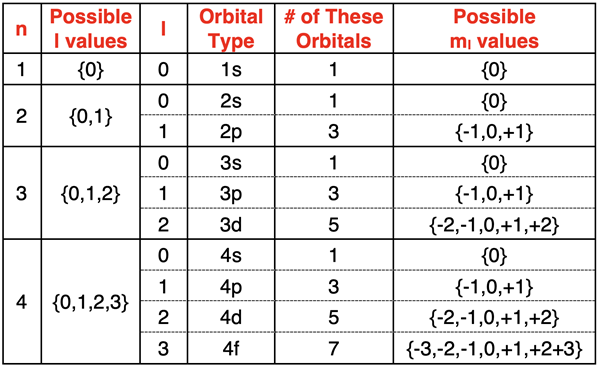
Electron Spin Quantum Number

The fourth quantum number is referred to as the electron spin quantum number and is represented by the symbol ms. The value of ms is independent of the value of any other quantum number. There are only two possible values for ms - +½ and -½. The ms value describes the direction of the electron’s spin. A clockwise spin direction is sometimes referred to as an up spin and assigned an ms value of +½. Spinning in the opposite direction (counter-clockwise) is referred to as a down spin and assigned an ms value of -½. According to the Pauli Exclusion Principle, no two electrons in an atom can have the same set of four quantum numbers. Two electrons with the same first, second, and third quantum numbers are located in the same atomic orbital. But they are distinguished from one another by their electron spin quantum number (ms). One has a +½ value and the other has a -½ value.

 

 

Do Electrons Really Spin?

We have a confession to make. An electron doesn’t spin … at least not in the sense that a top or an ice skater spins about an axis. What we do know is that the fourth quantum number has something to do with the magnetic field observed of the electron. The property is similar to the property that we might observe of a spinning charged particle. Thus, we loosely describe the electron as having spin. The fact is that an electron exhibits a quantized property associated with its magnetic field. There are two possible values, each associated with opposite magnetic properties.

 
 

 

 

 

Energy Levels

Previously in Lesson 2, we discussed the relative energy levels of the various orbitals in different electron shells. We mentioned that there is an energy overlap of the n=4 electron shell and the n=3 electron shell. That is, the 4s orbital (from the n=4 shell) is lower in energy than the 3d orbital (from the n=3 shell). We provided a rather cumbersome, graphical method of determining relative energy levels. Here we present a much easier way … at least, much easier if you understand quantum numbers.

The two quantum numbers that affect the overall energy of orbitals are n and l. According to quantum mechanics, the relative energy of orbitals can be predicted from knowledge of n and l. The rules are …

  1. Orbitals with the lowest n + l sum are lowest in energy.
  2. For two orbitals with the same n + l sum, the one with the lowest n value is lowest in energy.
     
 

Before You Leave

  1. Practice. Try our Quantum Mechanics Concept Builder. Any of the activities would make great practice!
  2. Download our Study Card on Quantum Numbers. Save it to a safe location and use it as a review tool. 
  3. The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding. 

 
 

 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. How many orbitals have a quantum number of ….

  1. n = 3? 
    Check Answer

     
  2. n = 4? 
    Check Answer

     
  3. n = 3 and l = 0? 
    Check Answer

     
  4. n = 3 and l = 1? 
    Check Answer

     
  5. n = 3 and l = 2? 
    Check Answer

     
  6. n = 4 and l = 2? 
    Check Answer

     
  7. n = 4 and l = 3? 
    Check Answer

     
  8. n = 3 and l = 1 and ml = -1? 
    Check Answer

     
 
2. What is the maximum number of electrons that can have the following quantum numbers?
  1. n = 2 
    Check Answer

     
  2. n = 3  
    Check Answer

     
  3. n = 2, l = 1  
    Check Answer

     
  4. n = 3, l = 1  
    Check Answer

     
  5. n = 3, l = 2  
    Check Answer

     
  6. n = 3, l = 1, ml = -1  
    Check Answer

     
  7. n = 3, l = 2, ml = +1  
    Check Answer

     
  8. n = 3, l = 2, ml = +1, ms = -½  
    Check Answer

     
 
 
3. Which of the following sets of quantum numbers are allowed?  If disallowed, indicate why.
  1. n = 2,  l = 2,  ml = 0,  ms = ½   
    Check Answer

     
  2. n = 3,  l = 1,  ml = -1,  ms = ½   
    Check Answer

     
  3. n = 4,  l = 2,  ml = 3,  ms = -½   
    Check Answer

     
  4. n = 2,  l = 0,  ml = 1,  ms = -½   
    Check Answer

     
  5. n = 3,  l = 2,  ml = -1,  ms = -½   
    Check Answer

     
  6. n = 2,  l = -1,  ml = 0,  ms = -½   
    Check Answer

     
 
 
4. Give a possible set of quantum numbers for an electron located in a …
  1. 2p orbital.    
    Check Answer

     
  2. 3s orbital.    
    Check Answer

     
  3. 3d orbital.    
    Check Answer

     
  4. 4f orbital.    
    Check Answer

     
  5. 2s orbital.    
    Check Answer

     
  6. 3p orbital.    
    Check Answer

     

 
 

 
 

 

 

Jump to Next Lesson: Electron Configurations

View: Chapter Contents