Lesson 1: Atomic Mass and Atom Counting

Part b: Measuring Atomic Mass

Part a: Atomic Mass
Part b: Measuring Atomic Mass
Part c: The Mole
Part d: Grams-Moles-Atoms Relationship

 

 

Average Atomic Mass

The atomic mass is the mass of one atom of any isotope. As we discussed in Lesson 1a, the periodic table lists the average atomic mass for each element. The average atomic mass is the mass of an average atom of that element. The unit is atomic mass units or amu. But what is an average atom?
 

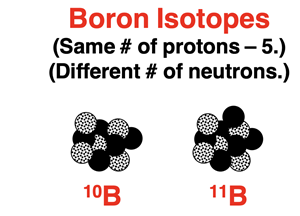
Most elements have two or more naturally occurring isotopes. Isotopes of an element have the same number of protons but a different number of neutrons. The varying number of neutrons for these isotopes means that each isotope has a different mass. So, an average atom is an atom that is a weighted average of all the isotopes of that element.
 
As an example, let’s consider the element boron. There are two naturally occurring isotopes of boron – boron-10 and boron-11. They each have five protons but either five or six neutrons. Individually, there masses are 10.0129 amu and 11.0093 amu respectively. The average atomic mass of boron is the weighted average of these two numbers. The percent abundance is the weighting factor. The value for the average atomic mass is 10.811 amu. We can reason that the boron-11 isotope is more abundant since the weighted average value is closer to its atomic mass. It is worthwhile to note that there isn’t a single atom in any sample of boron that has a mass of 10.811 amu. This value simply describes the weighted average of all boron atoms.
 
 

 

Atomic Mass Spectrometry

An atomic mass spectrometer is a device that can analyze a sample of an element to determine the relative abundance of isotopes and the mass of each isotope. The device consists of an ionizer that ionizes the isotopes in the sample by removing one or more electrons. The resulting ions of the isotopes have different mass-to-charge ratios (m/q). These ions are then accelerated and beamed towards a magnet. The magnet exerts a magnetic force upon the beam which deflects the ions from their otherwise straight-line path. The less massive isotopes will be deflected more than the more massive isotopes. The beam of ions is separated by the magnet into individual isotope streams. A detector collects the ions of each isotope separately. The electronics of the device is capable of determining the percentage of each isotope in the original sample and the relative mass of each isotope.  A sample output for the two lithium isotopes is shown in the graphic below.

 

 

 

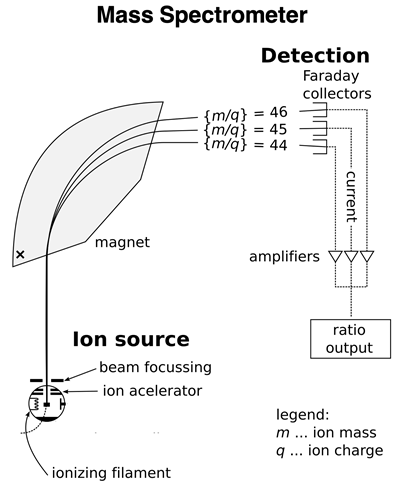
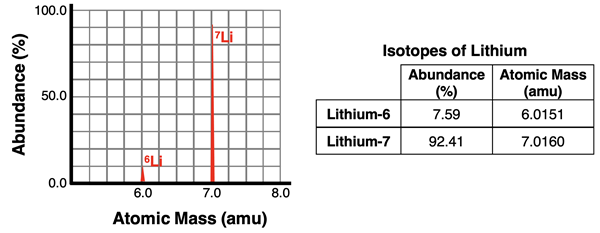
Image of Spectrometer: Public Domain

 
 
 

Analyzing Mass Spectrum Data

The data provided by a mass spectrometer can be used to calculate the average atomic mass of an element. For instance, the data for lithium (above) can be used to calculate the average atomic mass of lithium. Since the average atomic mass is a weighted average of the isotopes, the atomic mass of each isotope is multiplied by the fraction of that isotope found in the sample. The fraction is the percent abundance divided by 100.

Ave. Atomic Mass = (7.59/100)•(6.0151 amu) + (92.41/100)•(7.0160 amu)
 
Ave. Atomic Mass = 6.9400 amu

 
 
In general, the average atomic mass is calculated using the equation:
 

Ave. Atomic Mass = ( F₁*AM₁  +  F₂*AM₂  +  F₃*AM₃ ) / 100

 
where AM₁, AM₂, and AM₃ represent the atomic mass of isotopes 1, 2, and 3, and F₁, F₂, and F₃ represent the fraction (i.e., percent abundance/100) of isotopes 1, 2, and 3.

The two worked-out examples below demonstrate the use of this equation.
 
 
 

Example 1 - Boron

There are two naturally occurring isotopes of boron. A mass spectrometer determines the atomic mass and percent abundance of each isotope. The output data is shown at the right. Use this data to determine the average atomic mass of boron.
 

 
 
 

Example 2 - Chlorine

There are two naturally occurring isotopes of chlorine. A mass spectrometer determines the atomic mass and percent abundance of each isotope. The output data is shown at the right. Use this data to determine the average atomic mass of chlorine.
 

 

 

 

Before You Leave

• Download our Study Card on Average Atomic Mass. Save it to a safe location and use it as a review tool. 
• Our Calculator Pad section has a set of Practice Problems on the topic. Your answers are evaluated and feedback is provided; you have infinite opportunities to correct your mistakes. Try Problem Set PMG1.
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Lithium has an average atomic mass of 6.940 amu. How many atoms in a typical sample of lithium have an atomic mass of 6.940 amu?

 
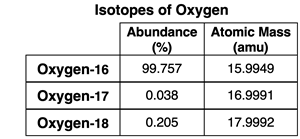
2. Use the mass spectrometer data at the right to determine the average atomic mass of oxygen.