Lesson 2: Concentration

Part a: Molarity

Part a: Molarity
Part b: Dilution
Part c: Percent by Mass and by Volume
Part d: Solution Stoichiometry

 

Concentration

A solution is composed of a solute dispersed about a solvent. One property of a solution is its concentration. Concentration describes the quantity of solute in a given amount of solution. A solution that has a relatively large quantity of solute in a given amount of solution is described as being concentrated. And solutions that have a relatively small quantity of solute in a given amount of solution is described as being dilute.

 
There are a variety of methods for quantifying the concentration of solute. We will discuss a couple of these in Lesson 2. A parts per million value indicates the number of parts of solute per every million parts of the solution. By "parts", we can mean either mass, volume, or particles. Molality values express concentration in terms of the moles of solute per kg of solvent. Percent by mass values indicate the mass of solute in grams per every 100 grams of solution. Percent by volume values indicate the volume of solute in liters per every 100 liters of solution. Perhaps the most common method (at least in a Chemistry course) of expressing concentration is by use of the concept of molarity, also known as molar concentration. Lesson 2a will focus on molarity.
 
 
 

Molarity

Molarity describes the concentration of a solution by experessing it in terms of the ratio of the moles of solute per every liter of solution. The mathematical equation for determining the molarity requires a knowledge of the number of moles of solute in a given volume of solution (in liters). The equation is

 
It is worth noting three things about the equation:

• Molarity is a ratio of two numbers - moles divided by volume.
• The volume must be in liters. If it is known in mL, then a conversion must be made.
• The denominator is the volume of solution. It is NOT the volume of the solvent. (Though in many cases, the solute makes a negligible contribution to the solution’s overall volume.)

 
 
 

Units and Labels

Based on the above equation, it is sensible to state that the unit of molarity is moles/liter. We often abbreviate moles/liter or mol/L by the symbol M. A 2.0 M solution is a solution concentrated with 2.0 moles of solute per every 1 liter of solution. Another unit of molarity is molar. Molar means the same thing as moles per liter or mol/L or M.  To describe a solution as being a 2.0 molar solution also means that there are 2.0 moles of solute per every 1 liter of solution.
 
As a student performs work for a Chemistry course, they quickly learn the importance of labeling the work. For instance, when calculating the density of a liquid to be 1.21 g/mL, they would report
   
The “Density =” or “d =” are the labels that describe the quantity that comes thereafter. Similarly, a student may calculate a pressure to be 769 mm Hg and report
   
“Pressure =” and “P = “ are labels that convey to the reader the type of quantity that is being reported.
 
Naturally, we would use a “Molarity = “ label to communicate the result of a molarity calculation. To report that the molarity of NaCl in an aqueous solution is 0.450 M, we would write
   
There is however a commonly used shorthand notation that we will use throughout this Chemistry Tutorial. It involves writing the name of the solute and enclosing it in square brackets. So, [NaCl] means the molarity of NaCl. We might write
   
 
 

Making Meaning of Molarity

Molarity is a ratio. The statement [NaCl] = 0.450 M is not asserting that there is a solution with a volume of 1 liter and it contains 0.450 moles of NaCl. Instead, it is stating that the ratio of moles of solute to liters of solution is 0.450. Grasping the concept of what molarity means is every bit as important as being able to plug numbers into a calculator and determining its value. Here is some (hopefully) head-math styled statements that will help you process the meaning of the molarity concept.
 
A 2.0 M NaCl solution having a volume of …

• … 1.0 L contains 2.0 mol of NaCl.
• … 0.50 L contains 1.0 mol of NaCl.
• … 1.2 L contains 2.4 mol of NaCl.

 
A 0.50 L solution of NaCl that contains ….

• … 2.0 mol of NaCl has a molarity of 4.0 M.
• … 0.50 mol of NaCl has a molarity of 1.0 M.
• … 1.0 mol of NaCl has a molarity of 2.0 M.

 
A solution containing 2.0 moles of NaCl will have a …

• … concentration of 1.0 M if its volume is 2.0 L.
• … concentration of 4.0 M if its volume is 0.50 L.
• … concentration of 0.50 M if its volume is 4.0 L.

 
You will find some more statements in the Check Your Understanding section for practice.
   
 

Solution Preparation

An aqueous solution is often prepared by dissolving a certain amount of solute in water until a specified volume of solution is obtained. Let’s suppose you were given the task of preparing 2.00 L of an aqueous solution of 1.50 M NaCl. How would you accomplish such a task? It might be obvious to many students that you would place 3.00 mol of NaCl into a calibrated container and add enough water (while stirring) until its final volume reached the 2.00 L mark. When you were done, there would be 3.00 moles of solute (NaCl) and 2.00 liters of solution and that would be equivalent to a 1.50 M solution. If this is your intuition of how to make a 1.50 M solution, then you are thinking correctly. But let’s fill in some of the details.
 
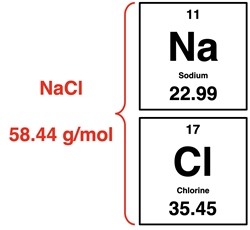
First, it is not possible to count out 3.00 moles of NaCl. One must determine the mass of NaCl that is equivalent to 3.00 mol NaCl and then measure out that amount of mass. The molar mass of NaCl is 58.44 g/mol. So, 3.00 moles of NaCl would be equivalent to 175.3 g NaCl.
 

 
The first step of this multi-step task involves massing out 175.3 g or NaCl to be added to the solution.
 
Second, the proper container for preparing a 2.00 L solution is known as a 2.00-L volumetric flask. Such a flask has a single marking at the 2.00 L mark. The basic idea is to add the measured solute to the flask, add water, and stir (or shake). Typically, water is added to a level at or below the narrow neck of the flask and the solute is dissolved. At that point, there will be an aqueous solution of NaCl. … just not 2.00 L of 1.50 M NaCl. Once dissolved, more water is added until the volume of the solution is 2.00 L. That is, add water until the 2.00-L mark is reached. At that point, there is 2.00 L of aqueous solution that contains 3.00 mol NaCl; and that is exactly a 1.50 M solution. The procedure is shown in the diagram below.
   
 
 

Relating Mass, Moles, Volume, and Molarity

The equation described above can be named the molarity equation. It is the perfect equation for calculating the molarity of a solution (M) if you know the number of moles of solute (n_solute) and the volume of solution (V_solution). The equation is set up to calculate M. But often times, you need to calculate the number of moles of solute (n_solute) or the volume of solution (V_solution). Thankfully, algebra allows us to do so. The equation can be rearranged to form a moles equation or a volume equation as shown below.
   
The equation that is used depends on what quantity needs to be calculated.
 
It is often necessary to relate the mass of the solute to the molarity, the volume of solution, or the number of moles of solute. While the mass is not part of the molarity equation, it is directly related to the number of moles of solute (n_solute). Using the molar mass of the solute, conversions can be made between the grams and the moles of solute. An equation or an additional conversion can be used to calculate a molarity or a volume. These relationships are shown in the graphic organizer below. Examples 1, 2, and 3 demonstrate how they are used in the context of a typical chemistry problem.
     
 

Example 1

What mass of NaNO₃ must be added to water to make 5.00 L of a 0.500 M aqueous solution?
 
 

Solution

The diagram below illustrates what we know (molarity and volume) and what we wish to determine (mass of solute).
   
Solving this problem will involve two steps. First, we will use the molarity and volume to determine the moles of solute. Second, we will use the molar mass of the solute to determine the mass of the solute.
 
Step 1: The moles equation (above) can be used to determine the moles of NaNO₃ in the solution:
   
Step 2: The molar mass of NaNO₃ is 84.99 g/mol. The factor label method can be used to determine the mass of NaNO₃ that is equivalent to 2.50 mol.
   
 
 

Example 2

What is the molarity of a solution that is made by dissolving 11.01 g of lithium sulfate in water to make a 2.00 L solution?
 
 

Solution

The diagram below illustrates what we known (mass of solute, volume of solution) and what we wish to determine (molarity).
   
Solving this problem will involve two steps. First, we will use the molar mass of lithium sulfate (Li₂SO₄) to convert the mass of solute to the moles of solute. Second, we will use the moles of solute and the given volume of solution to determine the molarity of the solution.
 
Step 1: The solute is Li₂SO₄.The molar mass of Li₂SO₄ is 109.94 g/mol. The factor label method can be used to determine the moles of Li₂SO₄ that is equivalent to 11.01 g Li₂SO₄.
   
Step 2: The molarity equation (above) can be used to determine the molarity of  the solution. The unrounded value for the moles of Li₂SO₄ from Step 1 will be used in the calculation.
   
 
 

Example 3

Mrs. Friedmont has a bottle of 1.25 M solution of KCl. She needs to acquire 0.500 mol of KCl for a demonstration. What volume of the solution should she retrieve from the bottle?
 
 

Solution

The diagram below illustrates what we known (moles of solute, molarity of solution) and what we wish to determine (volume of solution).
   
The solution to this problem will involve a single step. The volume of the solution can be determined using the volume equation (above). 
   
 
 

Ion Concentrations

When we say the molar concentration of NaNO₃ is 2.50 M, we are describing how many moles of NaNO₃ were dissolved per 1 liter of solution. But we know from Lesson 1 that the particles present in solution are not NaNO₃ particles. Rather, the particles are the ions of NaNO₃. It is Na⁺ and NO₃^- ions that are in the solution. While knowing the concentration of NaNO₃ is useful, it is often more important to know the ion concentration.
 
The ion concentration can be determined from the formula of the ionic compound and its concentration. In Lesson 1e, we learned how to determine the number of cations and the number of anions formed by the dissociation of the ionic compound. In the case of NaNO₃, there is one Na⁺ ion and one NO₃^- ion formed by the dissociation of one formula unit of the ionic compound.
   
Since the dissociation of 1 mole of NaNO₃ forms 1 mole of Na⁺ ion and 1 mole of NO₃^- ions, the ion concentrations will be equal to the concentration of the NaNO₃.
   
The situation becomes a bit more complicated for an ionic compound such as Al₂(SO₄)₃. Aluminum sulfate dissociates into two Al³⁺ ions and three SO₄^2- ions.
   
Since the dissociation of 1 mole of Al₂(SO₄)₃ forms 2 moles of Al³⁺ ions and 3 moles of SO₄^2- ions, the ion concentrations will not be equal to the concentration of the Al₂(SO₄)₃. Rather, the Al³⁺ concentration will be two times greater than the Al₂(SO₄)₃ concentration and the SO₄^2-concentration will be three times greater than the Al₂(SO₄)₃ concentration.
   
Determining the ion concentrations from the concentration of the ionic compound begins by writing the dissociation equation for the ionic compound. Then the coefficients can be used as multipliers to determine the ion concentrations.
 
 
 
Example 4
The table lists dissolved salts and their molar concentrations. Use the table format to determine the corresponding ion concentrations. Review our Tutorial page on Dissociation of Ionic Compounds if you need assistance determining the number of ions in each salt.  

Solution

 
 
 
 

Before You Leave

• Download our Study Card on Molarity. Save it to a safe location and use it as a review tool.  (Coming soon.)
• We have two Concept Builders that will provide great practice with internalizing the ideas of this lesson. They include: Molarity Ranking Tasks and Molarity Calculations.
• When it comes to solving Chemistry problems, our Calculator Pad is an awesome location for perfecting your skills. Try any one of the following sets of problems to level up you molarity skills: Introduction to Molarity || Molarity Calculations 1 || Molarity Calculations 2 || Molarity Calculations 3 ||  Ion Concentrations 1 || Ion Concentrations 2
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
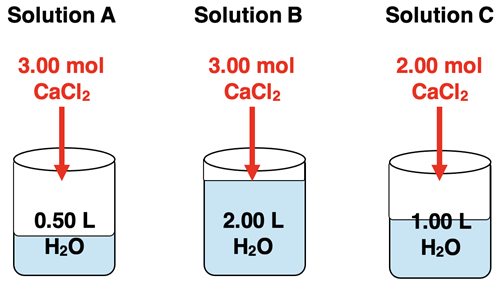
1. Three aqueous solutions are made by mixing varying amounts of solute (CaCl₂) in the same volume of water. Rank the solutions according to their molarity (M).

 


 
2. Three aqueous solutions are made by mixing the same amounts of solute (CaCl₂) in the varying volumes of water. Rank the solutions according to their molarity (M).

​

 

 
3. Three aqueous solutions are made by mixing varying amounts of solute (CaCl₂) in the varying volumes of water. Rank the solutions according to their molarity (M).

​

 

 

 
4. Describe in words the meaning of the following symbols:

1. [CaCl₂] = 2.00 M 
   
   Check Answer
   Answer: 
   [CaCl₂] = 2.00 M refers to an aqueous solution with a molarity (or molar concentration) of 2.00 M. That is, there is 2.00 mole of CaCl₂ per every 1 L of solution. 
   
   
    
   
    
2. 3.15 M Al₂(SO₄)₃ 
   
   Check Answer
   Answer: 
   3.15 M Al₂(SO₄)₃ refers to an aqueous solution whose solute is aluminum sulfate. The 3.15 M refers to the molarity or molar concentration of the solution. It means that there is 3.15 moles of Al₂(SO₄)₃ per every 1.00 L of solution.
   
    
   
    
3. [Ca²⁺] = 0.400 M 
   
   Check Answer
   Answer: 
   [Ca²⁺] = 0.400 M refers to an aqueous solution of an ionic compound that contains calcium ions as the cation. The molarity or molar concentration of these ions is 0.400 M. That means there is 0.400 moles of Ca²⁺ ions in every 1.00 L of solution. No information is provided about the anion or the identity of the ionic compound.
   
    
   
    

 

 
5. Complete the following sentences by filling in the blanks.

1. A 2.0 L sample of a 3.0 M solution of NaF contains _____ mol of NaF. 
   
   Check Answer
   Answer: 6.0 mol
   
   If there are 3.0 mol per 1.0 L (that is, 3.0 M), then there must be 6.0 mol NaF for 2.0 L. 
   
    
    
    
2. A 0.500 L sample of NaCl that contains 1.50 moles of NaCl has a molarity of _____ M. 
   
   Check Answer
   Answer: 3.00 M
   
   Molarity is the ratio of moles of solute to liters of solution. Dividing 1.50 mol by 0.500 L yields 3.00 mol/L or 3.00 M.
   
    
   
    
3. A 1.5 M solution of CaSO₄ containing 0.50 moles CaSO₄ has a volume of ____ L. 
   
   Check Answer
   Answer: 0.40
   
   Molarity is the ratio of moles of solute per liter of solution. That ratio must be 1.5 since the molarity is 1.5 M. So the volume must be 0.40 L, so that 0.60 mol/0.40 L ratio comes out to be 1.5 mol/L.
   
    
   
    
4. A 200 mL solution of NaCl that contains 0.400 moles of NaCl has a molarity of _____ M. 
   
   Check Answer
   Answer: 2.00 M
   
   A 200 mL solution is a 0.200 L solution. The molarity is the moles of solute per liters of solution. So, divide the 0.400 moles by 0.200 L to get a molarity of 2.00 mol/L or 2.00 M.
   
    
   
    
5. There will be ______ moles of AgNO₃ in a 300.0 mL sample of 2.00 M AgNO₃. 
   
   Check Answer
   Answer: 0.600
   
   A 300.0 mL solution is a 0.3000 L solution. The number of moles can be determined by multiplying the volume in liters by the molarity. That results in 0.3000* 2.00 which is 0.600 moles.
   
    
   
    
6. If 0.50 mol of NaCl are needed, then you should retrieve ______ mL of a 2.0 M NaCl solution. 
   
   Check Answer
   Answer: 250 mL
   
   The molarity is the mole to liter ratio. If the molarity is 2.0 M, then there are 2.0 mol per every 1.0 L. a solute amount of 0.50 mol is one-fourth of the 2.0 mol that would be in a liter. If you want 0.50 moles, you need one-fourth of a L or 0.250 L. So 250 mL will provide 0.50 moles.
   
    
   
    

 

 
6. Expain with some detail how to make 500 mL of an aqueous solution of 2.00 M NaF.
 



 
7. Complete the following sentences by filling in the blanks.

1. If [Ca(C₂H₃O₂)₂] = 1.5 M, then [Ca²⁺] = ______ M and [C₂H₃O₂^-] = ______ M. 
   
   Check Answer
   Answer: 
   If [Ca(C₂H₃O₂)₂] = 1.5 M, then [Ca²⁺] = 1.5 M and [C₂H₃O₂^-] = 3.0 M.
   
    
   
    
2. If [AlF₃] = 0.50 M, then [Al³⁺] = ______ M and [F^-] = ______ M. 
   
   Check Answer
   Answer: 
   If [AlF₃] = 0.50 M, then [Al³⁺] = 0.50 M and [F^-] = 1.50 M. 
   
   
    
   
    
3. If [(NH₄)₂SO₄] = 0.50 M, then [NH₄⁺] = ______ M and [SO₄^2-] = ______ M. 
   
   Check Answer
   Answer:
   If [(NH₄)₂SO₄] = 0.50 M, then [NH₄⁺] = 1.00 M and [SO₄^2-] = 0.50 M.
   
    
   
    
4. If [AlPO₄] = 0.20 M, then [Al³⁺] = ______ M and [PO₄^3-] = ______ M. 
   
   Check Answer
   Answer:
   If [AlPO₄] = 0.20 M, then [Al³⁺] = 0.20 M and [PO₄^3-] = 0.20 M.
   
    
   
    

 

 
8. What is the molarity of a solution that is made by dissolving 42.5 g of lithium nitrate in water to make a 0.250 L solution?
 

 
9. What mass of NaNO₃ must be dissolved in 300.0 mL of water to produce a solution with a molarity of 0.300 M?