Lesson 3: Limiting and Excess Reactants
Part b: Solving Limiting Reactant Problems
Part a: Non-Stoichiometric Conditions
Part b: Solving Limiting Reactant Problems
Part c: Determining the Excess Amount
What is a Limiting Reactant?
Lesson 3 of our Stoichiometry Tutorial pertains to situations in which the reactants are present in amounts that are different than the mole ratios in the balanced chemical equation. Such situations are described as having non-stoichiometric conditions. Under such conditions, one of the reactants will be a limiting reactant and the other reactant will be an excess reactant. The limiting reactant is the reactant that is entirely consumed before the other reactant is entirely consumed. The limiting reactant is the reactant that would produce the least amount of product. In a stoichiometry calculation, the amount of the limiting reactant is used to calculate the amount of product produced. Lesson 3a provides a detailed discussion of these concepts and is recommended reading prior to this page.
Recognizing a Limiting Reactant Problem
There are many different types of stoichiometry problems. Confronted with the wide range of problem types, a common student question is: How can I recognize a limiting reactant problem? There are a couple of ways to recognize such a problem. The telltale sign of a limiting reactant problem is that the problem lists the amount of both reactants. The problem might read something like this:
If 24.1 g of N2 are combined with 6.58 g of H2, then how much ammonia can be synthesized by the reaction N2 + 3 H2 → 2 NH3?
If you observe in the problem statement that the amounts of both reactants are given, then you know that the problem falls into the category of a limiting reactant problem. In such a case, you will need to identify which reactant is limiting and perform calculations based on the amount of the limiting reactant.
Identifying the Limiting Reactant
There are numerous ways to determine the limiting reactant if both reactant amounts are given. We describe three methods below. We prefer Method 1. But we would emphasize that the method that you use is the method that makes the most sense to you.
Method 1 – Identifying the Limiting Reactant
The limiting reactant is the reactant that produces the least amount of product. So, one method of determining which reactant is limiting is to calculate how much product is produced by each given amount of reactant. Carry out two independent stoichiometry calculations of the amount of product. The reactant that results in the least amount of product is the one that is limiting.
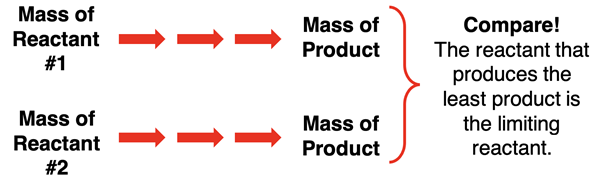
One bonus of this method is that the problem often requires that you determine how much product is produced. When using this method, you are determining the answer to the question of how much product is produced. If there are two products in the reaction, then perform calculations for the product that the problem focuses on (assuming it does).
When using this method, you will calculate two different product amounts – one based on each reactant amount. The amount of product that is produced is the smaller of the two product amounts. The larger amount is the amount that would be produced if there was a sufficient amount of the limiting reactant.
Method 2 – Identifying the Limiting Reactant
Our second method involves a single stoichiometry calculation. In the second method, choose either one of the two given amounts as the starting point of your calculation. We will refer to the one that you choose as being Reactant #1. Determine how much of the other reactant (Reactant #2) would be required to react completely with the amount of Reactant #1. Then ask if the given amount of Reactant #2 is greater than or less than the calculated amount that you need. If the given amount of Reactant #2 is greater than the calculated amount, then Reactant #1 is the limiting reactant and Reactant #2 is in excess. If the given amount of Reactant #2 is less than the calculated amount, then there is and insufficient amount of Reactant #2 and it is the limiting reactant.
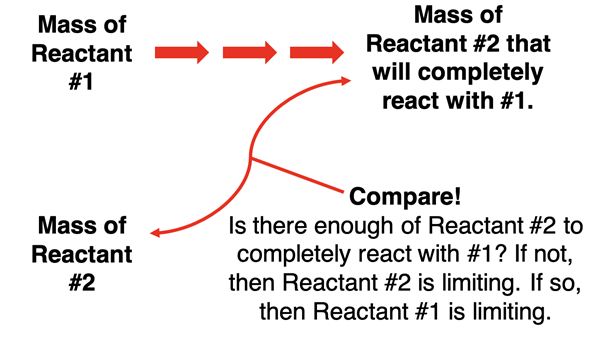
One bonus of this method is that you only have to carry out one stoichiometry calculation to determine which is the limiting reactant. A second bonus of this question is that it often serves as a useful calculation of how much excess reactant that there is. The downside of this method is you will need to do a second calculation in order to determine the amount of product produced (if that’s what the problem calls for).
Method 3 – Identifying the Limiting Reactant:
Our third method involves two calculations of the number of moles of each reactant and a lot of ratio thinking. Use the molar mass of each reactant to convert the given mass of reactant to the number of moles. Then use the coefficients of the balanced chemical equation to determine the mole ratio. Most students find it easiest to divide the larger coefficient by the smaller coefficient to get a mole ratio greater than 1. Now compare this mole ratio to the ratio of the moles of the two substances. By comparing the mole ratio (coefficient ratio) to the availability ratio (ratio of moles based on the given mass amounts), you can tell which is the limiting reactant.
The one upside of this method is that the gram-to-mole conversion is rather straightforward. One downside is that students need a strong conceptual grasp of mole ratios and their meaning. Another downside is that this method only determines which reactant is limiting. Unlike method 1 and 2, there is no bonus of having calculated the answer to any other question that the problem might ask.
Solving a Limiting Reactant Problem
A limiting reactant problem is a stoichiometry problem. Other than including the additional detail of having a second reactant amount, there is no difference between the stoichiometry problems of Lesson 2 and the limiting reactant problems of Lesson 3. Additionally, skill at solving a limiting reactant problem is acquired in the same way as it is for any stoichiometry problem. The skill is acquired through practice. Certainly, it helps to see some worked out examples. Our Tutorial pages provide plenty of that, like the two examples provided below. Watching someone else generate a solution to a problem is inferior to generating you own solution to a problem. You do not want the first time that you own a solution to be on test day. So, take advantage of the opportunities described in our Before You Leave section to acquire the skill of solving limiting reactant problems.
Example 1
If 24.1 g of N2 are combined with 6.58 g of H2, then how much ammonia can be synthesized by the reaction N2 + 3 H2 → 2 NH3?
The solution begins by determining the limiting reactant. The amount of product produced is based on the limiting reactant. Method 1 above is our go-to method. The bonus of using it is that we will have the answer to the problem once the limiting reactant is determined. The method involves using the mass of N
2 to determine how much NH
3 is produced and then repeating for the mass of H
2. Both calculations are three-step stoichiometry problems. We will need to know the molar mass of N
2, H
2, and NH
3 to perform the calculations.
The two different three-step, mass-to-mass conversions can now be performed. They are shown below:
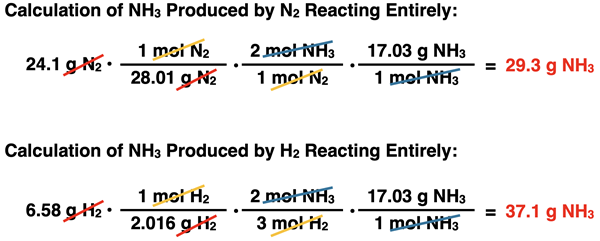
The two calculations above can be interpreted as follows. There is enough H2 present to produce 37.1 g NH3. But there is only enough N2 present to produce 29.3 g NH3. And so, the limiting reactant is N2 since it produces the least amount of product. The amount of NH3 produced is 29.3 g.
Example 2
Given: 2 Mg(s) + O2(g) → 2 MgO(s)
An ignition device combines 1.28 g of Mg with 1.02 g of O2. What is the limiting reactant and how much MgO is produced?
Like Example 1, the solution begins by determining the limiting reactant. We will use Method 1 again, knowing the bonus of using it is that we will have the answer to the problem once the limiting reactant is determined. The method involves using the mass of Mg to determine how much MgO is produced and then repeating for the mass of O
2. Both calculations are three-step stoichiometry problems. We will need to know the molar mass of Mg, O
2, and MgO to perform the calculations.
Now the two different three-step, mass-to-mass conversions can be performed. They are shown below:
The calculations show that there is enough O2 present to produce 2.57 g MgO. But there is only enough Mg present to produce 2.12 g MgO. And so, the limiting reactant is Mg since it produces the least amount of product. The amount of MgO produced is 2.12 g.
Determining the Amount of Excess Reactant
On the next page of Lesson 3, we will take these calculations one step further. We will determine how much of the excess reactant is remaining when the limiting reactant is used up.
Before You Leave
- Download our Study Card on Limiting and Excess Reactant Problems. Save it to a safe location and use it as a review tool.
- CalcPad - Stoichiometry Problem Sets: Problem Sets ST13 through ST15 include several limiting and excess reactant problems. Answer the question and receive immediate feedback and opportunities to correct your errors. Awesome follow up!
- The Check Your Understanding section below includes problems with solutions. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. Consider the synthesis of titanium (III) oxide from its elements.
4 Ti (s) + 3 O2(g) → 2 Ti2O3(s)
Determine the amount of Ti2O3 produced when 2.88 g of Ti are combined with 1.05 g O2.
2. Consider the reaction …
2 H2(g) + O2(g) → 2 H2O(l)
Determine the amount of H2O produced if 7.98 grams H2 are combined with 49.1 g O2.