The Physics Classroom » Chemistry Tutorial » Stoichiometry » Non-Stoichiometric Conditions

Lesson 3: Limiting and Excess Reactants

Part a: Non-Stoichiometric Conditions

Part a: Non-Stoichiometric Conditions
Part b: Solving Limiting Reactant Problems
Part c: Determining the Excess Amount


 

No Leftovers

Our Chapter on Stoichiometry has been concerned with the quantitative relationship between the amounts of reactants and products involved in a chemical reaction. Every situation has presumed that the moles of reactants and products that are available are present in ratios that match the ratio of their coefficients. For the reaction …

N2(g)  +  3 H2(g)  →  2 NH3(g)

… the mole ratio of N2 to H2 is 1 to 3 (1:3). That is, the number of moles of H2 that react is three times the number of moles of N2 that react. When the amount (in moles) of N2 and H2 that are available is 1:3, then all the N2 and all the H2 will react. We refer to these conditions as stoichiometric conditions. Under such conditions, all the reactants that are present in the reaction container will undergo a reaction. Neither reactant will be left over or remaining.
 
The table below demonstrates four instances of nitrogen and hydrogen availability matching the coefficient ratios. In each case, there will be no leftovers. Stoichiometric conditions means that neither reactant will be left over.

 
 
 

ICE Tables

ICE tables are a common conceptual tool used for bookkeeping. It is a tool for keeping track of the amount of reactants and products that are initially present, the amount of change that occurs as the result of the reaction, and the ending amount of reactants and product. ICE is simply a mnemonic for remembering the rows of the table – Initial Amount, Change Amount, and Ending Amount. Row a in the table above could be represented by the following ICE table:

 
As the top row of the ICE table shows, the starting substances are the reactants; there is no NH3 product initially present. As the middle row shows, the reactants are used up and the products are formed. This is the reason for the – signs in front of the change amounts for reactants and a + sign in front of the product. The numbers in this Change row are determined from the coefficients of the balanced chemical equation. The last row - Ending amount - is simply arithmetic. Add the Change amount (either a + or a -) to the Initial amount in order to determine the Ending amount.
 
A similar ICE table can be constructed for Row c:
 

 
 
 

Leftovers

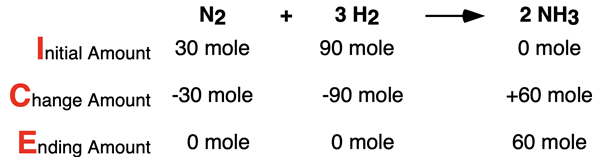
Now let’s consider what would happen if the amounts of N2 and H2 initially present in the reaction container were not present in stoichiometric amounts. That is, what would happen if the ratio of available N2 to H2 was not 1:3. In this discussion, we are making a distinction between the amounts that are available (the Initial Amount) and the amount that reacts (the Change Amount). You can always be certain that N2 and H2 will react in a 1:3 ratio, consistent with the coefficients of the balanced chemical reaction. But that does not mean that they are initially present in the reaction container in a 1:3 ratio.
 
Let’s suppose that there are 2 moles of N2 and 9 moles of H2 available. This is a 1:4.5 availability ratio and it does not match the 1:3 change ratio (i.e., the coefficients). A situation in which the availability ratio does not match the coefficient ratio is referred to as being a non-stoichiometric condition. When there are non-stoichiometric conditions, there will be a leftover reactant. One of the reactants will be used up and some of the other reactant will be left over. The ICE table is a great means of illustrating why there are leftovers.

 
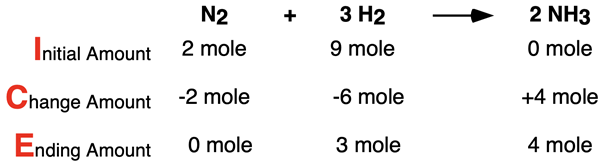
In this situation, there is more H2 initially available than is necessary. Only 6 moles is required to react with the 2 moles of N2. Since there is more than 6 moles of H2, not all of it reacts and there is some remaining at the end of the reaction.
 

 
 

 

Limiting and Excess Reactants

In the example discussed above, there is some H2 reactant remaining at the end of the reaction. We refer to the H2 as being an excess reactant. There is an excess of it available since there was more initially present as was necessary to react with all the available N2. It is also referred to as the leftover reactant since it is left over at the end. The N2 is referred to as the limiting reactant. The amount of N2 available limits how much product can be produced. As the reaction proceeds over the course of time, eventually the N2 becomes used up and cause the reaction to stop. The limiting reactant is the reactant that is used up first. If you look at the initial amounts that are available in the example, there is enough H2 to produce 6 moles of NH3. But 6 moles of NH3 are not produced because there is only enough N2 to produce 4 moles of NH3. The limiting reactant is the reactant that is available in an amount that produces the least amount of product.

 
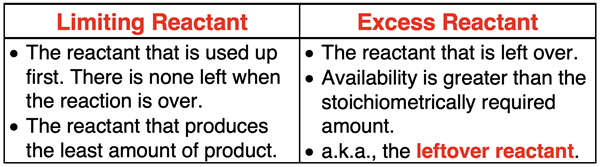
There are some common misconceptions with respect to limiting and excess reactants. First, the reactant that is the limiting reactant is dependent upon the amounts that are available. Just because N2 was the limiting reactant in one trial does not mean that it will be the limiting reactant in all trials. It simply depends on the amounts initially present in the reaction container.
 
Second, the limiting reactant is not necessarily the reactant that is least present. It is the reactant that produces the least amount of product. In a reaction such as N2  +  3 H2  →  2 NH3. There are three times as many moles of H2 required than N2. So, we would expect less N2 to be involved in the reaction. If there were 1.5 mole of N2 and 3.0 mole of H2, then H2 would be the limiting reactant even though there is less N2 available. Remove from your thinking any conception that the limiting reactant is the one that is least available. It is simply not true.
 
Third, not every trial of a reaction has a limiting and excess reactant. In our example reaction (N2  +  3 H2  →  2 NH3), if the two reactants are available with a 1:3 mole ratio, then we would describe the conditions as stoichiometric conditions. Under such conditions, both reactants are used up entirely and there is no excess reactant. Limiting and excess reactants are only a topic of discussion when the ratio at which reactants are available does not match the ratio of their coefficients in the balanced equation. Such conditions are referred to as non-stoichiometric conditions.
 

 
 

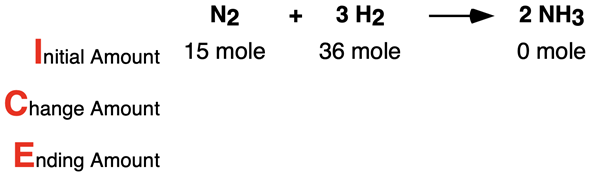
Example 1

Consider the following conditions for the reaction N2  +  3 H2  →  2 NH3. Determine the limiting reactant, complete the ICE table, and determine the number of moles of the excess reactant that remains. Tap the Check Answer button to check your understanding.



Check Answer

 

 
 

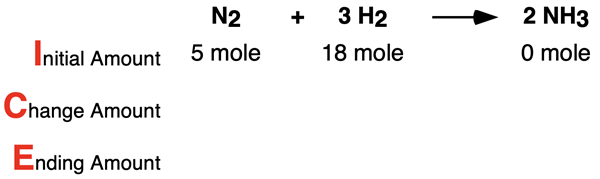
Example 2

Consider the following conditions for the reaction N2  +  3 H2  →  2 NH3. Determine the limiting reactant, complete the ICE table, and determine the number of moles of the excess reactant that remains. Tap the Check Answer button to check your understanding.




Check Answer

 
 
 

ICE Tables: Do the Mass

Our analysis thus far has pertained to the amounts of reactants in moles. More often, the amounts are expressed in grams. Moles and grams are related by the molar mass. A periodic table can be used to determine the molar masses of the two reactants and one product. Approximate values are:
 
            N2:  28.0 g/mol                      H2:  2.0 g/mol                        NH3:  17.0 g/mol
 
The ICE Table at the right is revised for mass values. Suppose that 56.0 g of N2 and 16.0 g H2 are initially available. What is the limiting and excess reactant? How much product is produced? How much excess reactant is left over?
 
All the logic that was used previously for moles can be carried over to this mass problem. Since the coefficients express the relative amounts of moles of each reactant and product involved in the reaction, we must do most of the math using moles. By dividing mass by molar mass, we can convert from grams to moles. Similarly, multiplying the number of moles by molar mass converts the moles to grams.
 
The given mass values are equivalent to having 2 moles of N2 and 8 moles of H2. The 2 moles of N2 would produce 4 moles of NH3. And the 8 moles of H2 would produce 5.3 moles of NH3. The limiting reactant is the reactant that produces the least amount of product. Thus, the N2 is the limiting reactant and H2 is the excess reactant.
 
Once the limiting reactant has been determined, the ICE table can be completed. The values are shown below.

 
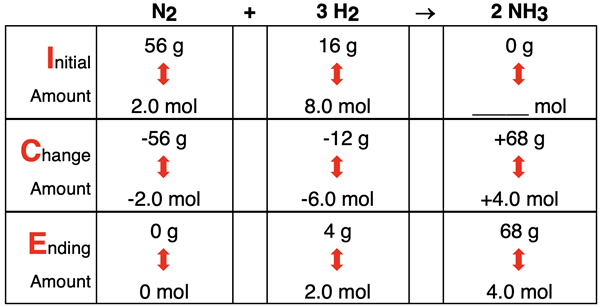
The amount of H2 that reacts is based on the amount of the N2 that reacts. This will always be the case. The amount of the excess reactant that is reacted away is based upon the amount of the limiting reactant that reacts. That’s why we call it the limiting reactant. It limits the amount of product that can be produced and the amount of reactant that reacts.
 
It is worthwhile to note that total system mass is conserved in any chemical reaction. That is, the total mass of reactants and products before the reaction is equal to the total mass of all reactants and products after the reactants. In this case, there are 72 grams initially (56 g + 16 g + 0 g) and 72 grams at the end of the reaction (0 g + 4 g + 68 g). This is one more example of the law of conservation of mass.
 

 
 

 

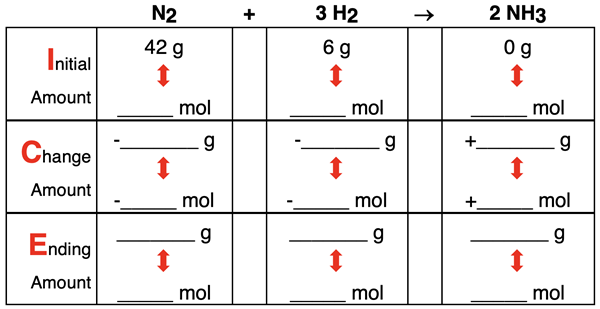
Example 3

Consider the following conditions for the reaction N2  +  3 H2  →  2 NH3. Determine the limiting reactant, complete the ICE table, and determine the grams of NH3 produced and grams of the excess reactant that remains. Tap the Check Answer button to check your understanding.




Check Answer

 
 
 

Before You Leave

  • Download our Study Card on Limiting and Excess Reactants. Save it to a safe location and use it as a review tool.
  • CalcPad - Stoichiometry Problem Set ST10: This set of 6 problems provides feedback and chances to correct errors. Each problem involves the use of an ICE table to analyze a limiting and excess reactant problem. The problem set makes an awesome follow up to this page!
  • The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Consider the following statements about limiting reactants. Identify each statement as being either TRUE or FALSE. For any False statement, identify what is wrong with the statement or correct the statement.
 
  1. The limiting reactant is the reactant that produces the least amount of product. 
    Check Answer

     
  2. The limiting reactant is the reactant that is present with the least amount of grams. 
    Check Answer

     
  3. The limiting reactant is the reactant that is present with the least amount of moles. 
    Check Answer

     
  4. The limiting reactant is the reactant that is used up first. 
    Check Answer

     
  5. The limiting reactant is the reactant that is listed first in the chemical equation. 
    Check Answer

     
  6. The limiting reactant is the reactant that is not left over when the reaction ends. 
    Check Answer

     
  7. The limiting reactant is the reactant with the smallest coefficient in the equation. 
    Check Answer

     
 
 
2. Consider the reaction …
2 H2 (g)   +   O2(g)   →   2 H2O(l)
 
For the given amounts of H2 and O2 initially present, identify whether the conditions are stoichiometric or non-stoichiometric conditions. If they are non-stoichiometric conditions, then identify the limiting reactant.
  1. 2 mol H2 and 1 mol O2  
    Check Answer

     
  2. 1 mol H2 and 2 mol O2  
    Check Answer

     
  3. 2 mol H2 and 2 mol O2 
    Check Answer

     
  4. 5 mol H2 and 2 mol O2 
    Check Answer

     
  5. 8 mol H2 and 5 mol O2 
    Check Answer

     
  6. 4 g H2 and 32 g O2 
    Check Answer

     
  7. 8 g H2 and 48 g O2 
    Check Answer

     
  8. 6 g H2 and 64 g O2 
    Check Answer

     

 
 
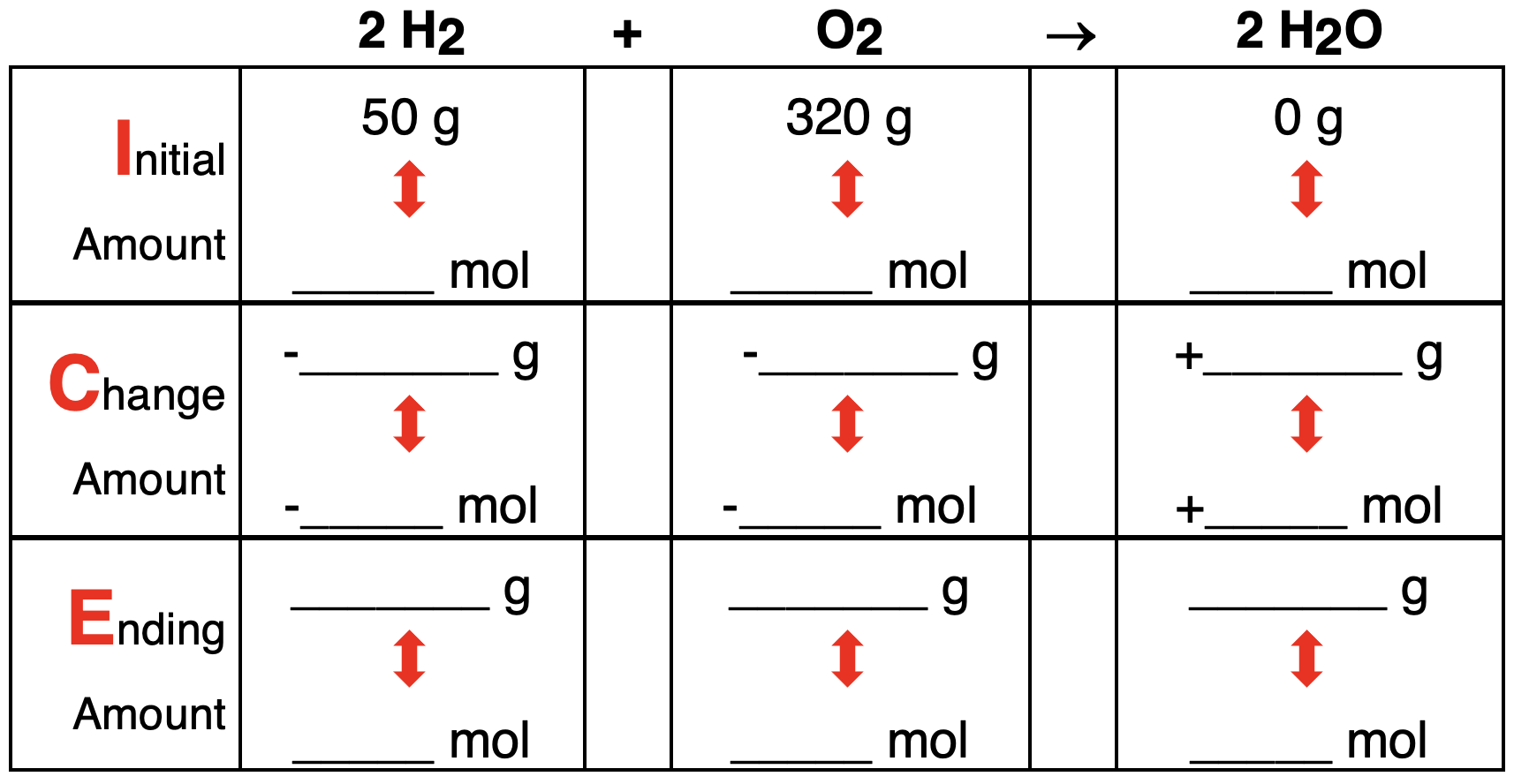
3. Consider the following conditions for the reaction 2 H2  +  O2  →  2 H2O. Determine the limiting reactant, complete the ICE table, and determine the number of moles of the excess reactant that remains. Tap the Check Answer button to check your understanding.

Check Answer

 
 
4. Consider the following conditions for the reaction 4 Ti  +  3 O2  →  2 Ti2O3. Determine the limiting reactant, complete the ICE table, and determine the number of moles of the excess reactant that remains. Tap the Check Answer button to check your understanding.

 

 

Check Answer

 
 

 
5. Consider the following conditions for the reaction 2 H2  +  O2  →  2 H2O. Determine the limiting reactant, complete the ICE table, and determine the number of moles of the excess reactant that remains. Tap the Check Answer button to check your understanding.

Check Answer

 

 

Next Part of this Lesson: Solving Limiting Reactant Problems

View: Chapter Contents