Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 1: A Framework for Thinking Stoichiometrically
Part a: Recipes, Ratios, and Relationships
Part a: Recipes, Ratios, and Relationships
Part b:
The Law of Conservation of Mass
Part c:
Conversions and Connections
 Bake a Cake
Bake a Cake
Let’s suppose you have plans to bake a cake for an upcoming event. How would you go about such a task? Would you simply toss several ingredients into a baking pan and put it in the oven? Or would you look for a recipe that called for specified amounts of certain ingredients to be measured and mixed before baking? Cooking, like Chemistry, occurs best when the ingredients are mixed together in specified amounts.
Here is a typical cake recipe, expressed as a cooking equation.

 The recipe includes information about the ingredients that are needed and the relative amounts of each ingredient. Some recipes may even provide additional information about the state of the ingredients. For instance, if walnuts were included, it might specify whether the walnuts were “whole” or “halved” or “crushed”. If bananas were included as an ingredient, it might specify “ripe” or “mashed”. These extra specifications might be described as the state or status of the ingredient. The final bit of information has to do with the amount of cake produced. The recipe might state that the cake will be large enough to provide 12 servings.
The recipe includes information about the ingredients that are needed and the relative amounts of each ingredient. Some recipes may even provide additional information about the state of the ingredients. For instance, if walnuts were included, it might specify whether the walnuts were “whole” or “halved” or “crushed”. If bananas were included as an ingredient, it might specify “ripe” or “mashed”. These extra specifications might be described as the state or status of the ingredient. The final bit of information has to do with the amount of cake produced. The recipe might state that the cake will be large enough to provide 12 servings.
Suppose the cook on a large ship wishes to use the above recipe to bake 20 cakes for the guests and crew. This is quite simple to do and doesn’t require a new recipe. It simply requires a scaling factor. To make 20 cakes, the cook would need to scale the recipe by a factor of 20. That is to say, the amount of each ingredient should be 20 times more than the amount listed in the recipe. That is what is meant by relative amounts. The cook would need 40 eggs, 20 cups of sugar, 10 cups of milk, etc. Recipes allow a cook to make how much? decisions. And those decisions are critical to the success of the recipe.
Chemical Equations are Like Recipes
A chemical equation is very much like a recipe for a chemical reaction. It lists the ingredients (formulae), the relative amounts (coefficients), and the state of the ingredients (state symbols). It also identifies the product(s) and product amounts. Chemical equations allow a Chemistry student to make how much? decisions.
Recipes indicate the amount of required ingredients using units such as cups, tablespoons, teaspoons, etc. Chemical equations list amounts using coefficients. Like recipes, the coefficients indicate the relative amounts of reactants and products in terms of particles. A particle could mean an atom (of an element), a molecule (of a molecular compound), or a formula unit (of an ionic compound).
Consider this reaction for the synthesis of ammonia (NH3).
N2(g) + 3 H2(g) → 2 NH3(g)
The reaction can be read as 1 molecule of nitrogen gas reacts with 3 molecules of hydrogen gas to produce 2 molecules of ammonia gas. The 1, 3, and 2 are the coefficients and indicate the ratios at which the reactants and products are involved in the reaction. The N2-H2 particle ratio is 1:3. The N2-NH3 particle ratio is 1:2. The H2-NH3 particle ratio is 3:2. These ratios help Chemistry students to make how much? decisions.
Like the cook on the ship, we could supersize this recipe by any whole number. If we wanted 20 molecules of ammonia, then we would simply use a scaling factor of 10:
10 N2(g) + 30 H2(g) → 20 NH3(g)
Molecules are quite small and 20 molecules is hardly even measurable so perhaps we would prefer to scale by one million:
1 x106 N2(g) + 3 x106 H2(g) → 2 x106 NH3(g)
Wait! Molecules are really, really, really small. We need a scaling factor much bigger than one million. Can you think of a suitable scaling factor for particles that would scale the number of particles so that it becomes measurable? Read on.
The Ideal Superizing Factor
Since coefficients indicate relative amounts, they can be scaled by whatever factor is needed … as long as each coefficient is scaled by the same factor. The most convenient factor by which to scale the coefficients is Avogadro’s number – 6.022x1023. It may seem quite strange to call this a convenient factor given both its enormity and the clumsiness of entering it on a calculator. But we are going to stick with our claim and here's our reasoning why:
Scaling the ammonia synthesis equation by Avogadro’s number results in
6.022 x 1023 N2(g) + 18.066 x 1023 H2(g) → 12.044 x 1023 NH3(g)
The unit associated with these numbers is molecules of N2, H2, and NH3. As we learned in Chapter 7, Avogadro’s number tell us the number of things in 1 mole of things. The mole is the counting unit of Chemistry. So, the 6.022 x 1023 molecules of N2 is equivalent to 1 mole of N2. The 18.066 x 1023 molecules of H2 is equivalent to 3 mole of H2. And the 12.044 x 1023 molecules of NH3 is equivalent to 2 mole of NH3. The above equation can be read to say
1 mole of N2 gas reacts with 3 mole of H2 gas to produce 2 mole of NH3 gas.

In equation form, this statement can be written as
N2(g) + 3 H2(g) → 2 NH3(g)
where the unit for the coefficients 1, 3, and 2 is the mole. Now that’s convenient!
Using the supersizing factor of Avogadro’s number, the coefficients of any chemical equation indicate the relative number of moles of reactants and products involved in the reaction. The particle ratios are also mole ratios.

Mole Ratios and Mass Ratios
We learned in Chapter 7 that the atomic mass values of the periodic table indicate the mass of an element on a per mole basis. We refer to it as the molar mass. So, 1 mole of hydrogen atoms (H) has a mass of approximately 1.0 grams (more precisely, 1.0079 grams). And 1 mole of diatomic hydrogen (H2) has a mass of approximately 2.0 grams. Using similar logic, we can assert that 1 mole of diatomic nitrogen (N2) has a mass of approximately 28 grams. And 1 mole of ammonia (NH3) has a mass of approximately 17 grams.
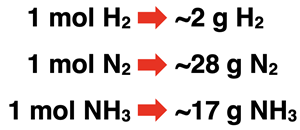
By supersizing the coefficients from molecules to moles, we are one short step away from relating the number of reactants and products in terms of grams. The molar masses of H2, N2, and NH3 can be used to transition from moles to grams. The table below shows these relationships.

We are now equipped with three types sets of relationship for making make how much? decisions. The coefficients 1, 3, and 2 allow us to relate the relative number of particles involved in the reaction. They also allow us to relate the relative number of moles involved in the reaction. And finally, by combining the coefficients with molar mass information, we can relate the relative mass (in grams) that are involved in the reaction.
 The Meaning of Stoichiometry
The Meaning of Stoichiometry
The title of this unit is Stoichiometry. It is a fancy word that is based on two Greek words joined together: Stoicheion + metron. The word stoicheion means element. And the word metron means to measure. Stoichiometry is concerned with measurements of elements involved in chemical reactions. Stoichiometry is the study of the quantitative relationship between the amounts of reactants and products involved in a chemical reaction. Stoichiometry focuses on the how much? questions of Chemistry. The Stoichiometry chapter will be one of the more heavily mathematical chapters in our Chemistry Tutorial.
<Pep Talk>
Chemistry students do best with this topic when they make sense of the logic behind the math and learn the skills for doing the math. In Lesson 1, we are making a strong effort to get you thinking about the relationships between quantities. We want you to understand coefficients, scaling factors, the concept of relative ratios of reactants and products, and mole-to-gram relationships. It’s indeed mathematical. But it is also sensible. Keep your sense-making ability active throughout the unit.
 In Lesson 1c, we will review an important tool introduced in Chapter 1 of our Chemistry Tutorial – the factor label method. The factor label method (or as many students of Chemistry call it: conversion factors) is the skill that we will use for doing the math. It is a method that works for easy problems and (even more charmingly) for hard problems. It is a method that works in Chapter 1, in Chapter 7, in Chapter 9, and in every other chapter of our Tutorial. The sooner you become comfortable with it, the more you can take advantage of its usefulness. Do everything you can to learn this skill. We’ve made it to the end of this course enough times to confidently advise you that it is a skill that isn’t going away. The moral of the story is to invest in learning how to use conversion factors early and the return on your investment will be much appreciated.
In Lesson 1c, we will review an important tool introduced in Chapter 1 of our Chemistry Tutorial – the factor label method. The factor label method (or as many students of Chemistry call it: conversion factors) is the skill that we will use for doing the math. It is a method that works for easy problems and (even more charmingly) for hard problems. It is a method that works in Chapter 1, in Chapter 7, in Chapter 9, and in every other chapter of our Tutorial. The sooner you become comfortable with it, the more you can take advantage of its usefulness. Do everything you can to learn this skill. We’ve made it to the end of this course enough times to confidently advise you that it is a skill that isn’t going away. The moral of the story is to invest in learning how to use conversion factors early and the return on your investment will be much appreciated.
</Pep Talk>
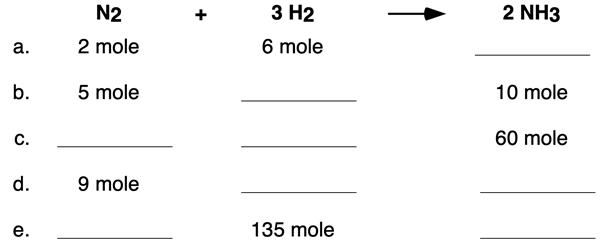
Example 1
We offer two multi-part examples in the form of table completion questions. Example 1 includes a table that pertains to moles. Use the coefficients of the equation to determine the missing cells of the table. Tap the View Answer button to view all missing cells and the logic by which their values were determined.
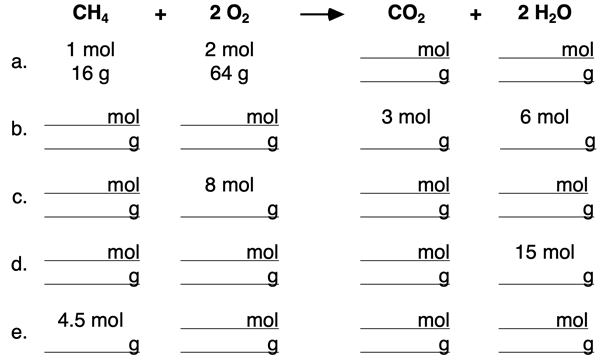
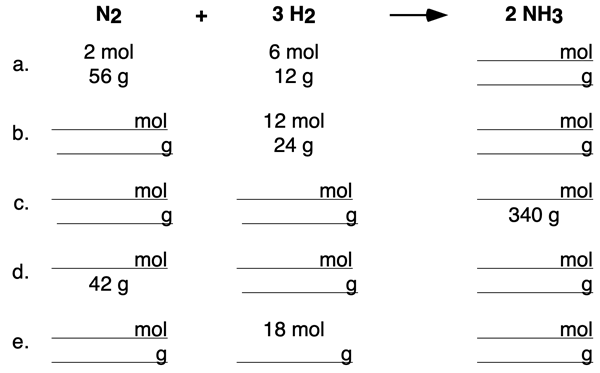
Example 2
Example 2 includes a table that pertains to both moles and grams. Use the coefficients of the equation and molar mass values to determine the missing cells of the table. Tap the View Answer button to view all missing cells and the logic by which their values were determined.
Before You Leave
- Download our Study Card on Stoichiometry Ratios. Save it to a safe location and use it as a review tool.
- Our Calculator Pad tool is a great place to practice any skill involving calculations. Try our Problem Set ST1, Introduction to Stoichiometry.
- Try our Stoichiometry: Relationships Concept Builder. Demonstrate your understanding of the relationships between moles and mass by completing a table similar to the above.
- The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. For the following chemical equations, provide a verbal description in terms of particles (atoms, molecules, and formula units).
Example: N2(g) + 3 H2(g) → 2 NH3(g)
is described by the statement: 1 molecule of nitrogen gas reacts with 3 molecules of hydrogen gas to produce 2 molecules of ammonia gas.
- 2 Al(s) + 3 Br2(l) → 2 AlBr3(s)
- 4 Na(s) + O2(g) → 2 Na2O(s)
- 2 NaCl(aq) + F2(g) → Cl2(g) + 2 NaF(aq)
2. Consider this balanced equation: 4 Na(s) + O
2(g) → 2 Na
2O(s)
Complete the following statements. (“mol” is the abbreviation for mole)
- For every 4 mol of Na that react, _____ mol of Na2O will be produced.
- For every 2 mol of Na that react, _____ mol of Na2O will be produced.
- For every 8 mol of Na that react, _____ mol of Na2O will be produced.
- For every 20 mol of Na that react, _____ mol of Na2O will be produced.
- For every 10 mol of Na that react, _____ mol of Na2O will be produced.
- For every 3 mol of Na that react, _____ mol of Na2O will be produced.
3. Consider this balanced equation:
CH
4(g) + 2 O
2(g) → CO
2(g) + 2 H
2O(g)
Use a periodic table and the equation to answer the following questions.
- Determine the molar mass of CH4.
- Determine the molar mass of O2.
- Determine the molar mass of CO2.
- Determine the molar mass of H2O.
- Determine the mole ratio of CH4:O2.
- Determine the mass ratio of CH4:O2.
- Determine the mole ratio of CH4:CO2.
- Determine the mass ratio of CH4:CO2.
- Determine the mole ratio of CH4:H2O.
- Determine the mass ratio of CH4:H2O.
4. Use the mole ratios to complete the blanks in the following table.
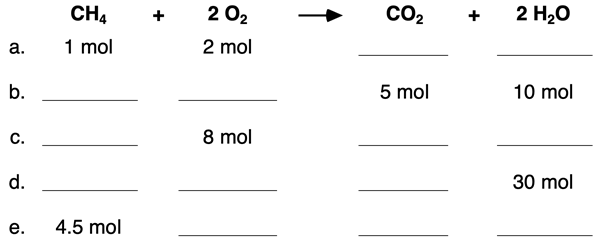
5. Use the mole ratios and molar mass values to complete the blanks in the following table.