The Physics Classroom » Chemistry Tutorial » Stoichiometry » Mole-to-Mole Relationships

Lesson 2: Relating Stoichiometric Quantities

Part a: Mole-to-Mole Relationships

Part a: Mole-to-Mole Relationships
Part b: Mole-to-Mass Relationships
Part c: Mass-to-Mass Relationships
Part d: Percent Yield
Part e: Stoichiometry Plus

 

The Stoichiometry Problem

Lesson 2 will include a collection of stoichiometry problems. The problems will provide a balanced chemical equation and an amount of a reactant or product. There will be a question about how much reactant or product would react or be formed based on the provided information. Solving the problems require that you utilize conversion factors (the factor label method). The problems will range in difficulty from one step problems (one conversion factor) to three step problems (three conversion factors).
 
The problems on this page are one step problems. You will be given the moles of reactant or product. And you will be asked to solve for the moles of another reactant or product. Only one conversion factor will be needed. The problems will look like this one:

Given:  N2(g)  +  3 H2(g)  →  2 NH3(g)
Determine the moles of NH3 produced from the reaction of 3.85 moles of N2.
 
We have highlighted in red the given quantity (3.85 moles of N2) and the desired quantity (moles of NH3).
 
 

 

Having a Plan

Lesson 1 of this chapter focused upon understanding the relationship between stoichiometric quantities. We spent a lot of time discussing the coefficients and mole ratios. We discussed molar mass and grams-to-mole relationships. And we introduced Mole Island.

 
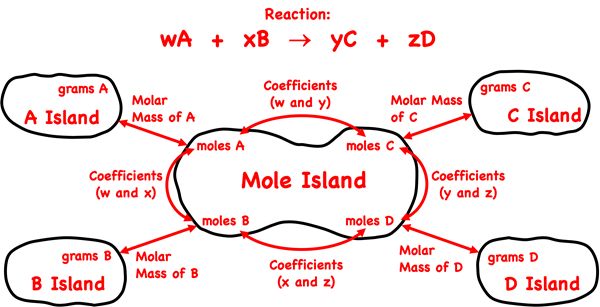
Mole Island is a graphic organizer that helps a student develop a plan for navigating their way through a problem. Mole Island shows what is related to what and how it is related. The graphic above is based on a reaction with generic reactants A and B and products C and D. The coefficients in the balanced equation are w, x, y, and z. The mass (in grams) and the moles of each reactant and product are identified on the diagram. Arrows connect these quantities. Each arrow represents a conversion step. One conversion factor is required per arrow. The words next to the arrows (Molar Mass, Coefficients) indicate the information that will be used in the conversion factor.
 
Mole Island can be used to develop a conversion plan between the given quantity and the desired quantity. Identify the location of the given quantity – grams or moles of reactant or product – on the diagram. Identify the location of the desired quantity – grams or moles of reactant or product. The arrows show the conversion pathway. If there are two arrows between the given and the desired quantities, then the solution to the problem will require two conversion steps.
 

 
 

The Mole-to-Mole Conversion

We will see how to use Mole Island to solve the problem:

Given:  N2(g)  +  3 H2(g)  →  2 NH3(g)
Determine the moles of NH3 produced from the reaction of 3.85 moles of N2.
 
We have redone Mole Island to reflect the specific reaction for the synthesis of ammonia (NH3).
 
We have identified the given quantity on the diagram (moles N2). We have also identified the desired quantity (moles NH3). There is one arrow between them and so the solution will require only one conversion factor. The words above the arrow indicate that the coefficients in front of N2 and NH3 in the balanced equation will be used in the conversion factor.
 
We begin our solution by writing down the given quantity with its unit. (Moles is abbreviated as mol.) This is a unit conversion problem; units are critical. It makes no sense to ignore units when the whole problem comes down to converting units. Our next step is to set up our one and only conversion factor. We place moles of N2 in the denominator of the conversion factor. A unit in the denominator will cancel the identical unit on the given quantity (or the identical unit in the numerator of another conversion factor). Mole Island indicated that moles of N2 is related to the moles of NH3. So, we place moles of NH3 in the numerator. This is our desired quantity. This unit is not cancelled, making it the unit on our answer.
 
Now we use the balanced chemical equation to place numbers in our conversion factor. In the chemical equation, there is a 2 in front of NH3. We place this number in the numerator with mol NH3. The coefficient in front of N2 in the balanced equation is understood to be a 1 since it is not displayed. We place a 1 in the denominator with mol N2. We can now reach for our calculator and do the math. The math involves multiplying the numerical value of the given quantity (3.85) by the number in the numerator (2) and dividing by the number in the denominator (1).
 
 
You may be thinking (always allowed): “this is a pretty simple problem to be doing all that work.” And you’re right. It is a simple problem and it is a lot of work. But as problems get more difficult, the conversion factor work will provide tremendous dividends and likely simplify the solution. Our practice will be to show how to use conversion factors on the easy problems (when they may not be needed) so that they can be more easily implemented on the harder problems (when they are very much needed). Once learned, the conversion factor method is as easy for a 3-conversion problem as it is for a 1-conversion problem. Doing the math in your head is considerably more difficult for a 3-conversion problem than a 1-conversion problem. Learn to use conversion factors!
 
We present two more examples below. Follow along to comprehend the approach. Then test your understanding using one or more of the suggestions in the Before You Leave section.
 

 

 

Example 1

Given:  3 Ti(s)  +  2 N2(g)  →  Ti3N4(s)
Determine the moles of Ti3N4 produced from the reaction of 4.92 moles of Ti.

 We will begin with plotting out a plan using Mole Island. The given quantity is the moles of Ti. This is a reactant in the chemical equation. We will call it substance A on Mole Island. The desired quantity is the moles of Ti3N4. This is a product in the chemical equation. We will call it substance C on Mole Island.
 
There is one arrow between moles A and moles C in the graphic. So, this a one conversion factor problem. It indicates above the arrow that coefficients will be used in the conversion factor. We will set up our conversion factors with units first. We list the given quantity (4.92 moles of Ti) and set up the conversion factor as a multiplier with a numerator and a denominator. We place mol Ti in the denominator to cancel the unit on the given quantity. We know from Mole Island that the moles of Ti is related to the moles to Ti3N4. So, we use mol Ti3N4 as the unit in the numerator. Since mol Ti3N4 isn’t cancelled, it is the unit on the answer. The conversion factor setup is shown below.
 
 
Now it’s time to insert numbers into the conversion factors. The numbers are the coefficients in the balanced chemical equation. The coefficient in front of Ti is 3 so the 3 goes in the denominator with the unit mol Ti. The coefficient in front of Ti3N4 is understood to be a 1 since it is not displayed. The 1 goes in the numerator with the mol Ti3N4. Reach to retrieve you calculator and do the math. Multiply the numerical value of the given quantity (4.92) by the value in the numerator (1) and divide by the value in the denominator (3).
 



 
 

 

 

Example 2

Given:  3 Ti(s)  +  2 N2(g)  →  Ti3N4(s)
Determine the moles of N2 that will react with 4.92 moles of Ti.

 
Once more the solution begins by plotting out a plan using Mole Island. The given quantity is the moles of Ti. Since this is a reactant in the chemical equation, we will call it substance A on Mole Island. The desired quantity is the moles of N2. This is also a reactant in the chemical equation. We will call it substance B on Mole Island.
 
There is one arrow between moles A and moles B in the graphic. This a one conversion factor problem. It indicates to the left of the arrow that coefficients will be used in the conversion factor. We will set up our conversion factors with units first. We list the given quantity (4.92 moles of Ti) and set up the conversion factor as a multiplier with a numerator and a denominator. We place mol Ti in the denominator to cancel the unit on the given quantity. We know from Mole Island that the moles of Ti is related to the moles to N2. So, we use mol N2 as the unit in the numerator. Since N2 isn’t cancelled, it is the unit on the answer. The conversion factor setup is shown below.
 
Now it’s time to insert numbers into the conversion factors. The numbers are the coefficients in the balanced chemical equation. The coefficient in front of Ti is 3 so the 3 goes in the denominator with the unit mol Ti. The coefficient in front of N2 is a 2. The 2 goes in the numerator with the mol N2. Reach to retrieve you calculator and do the math. Multiply the numerical value of the given quantity (4.92) by the value in the numerator (2) and divide by the value in the denominator (3).
 
 
 

 

 

A Step-by-Step Procedure

For some students, a step-by-step procedure is helpful. The procedure below describes what we have done in the above examples.

  1. Identify the given quantity (with unit) and the desired quantity in the problem statement.
  2. Locate the given quantity and the desired quantity on Mole Island. Then use their location to determine a conversion pathway. This includes determining the number of conversion factors needed and what information (coefficients or molar mass) will be included in the conversion factors.
  3. Set up your conversion factor: List the given quantity (with unit). Set up the conversion factor as a multiplier with a numerator and a denominator. The unit in the denominator is identical to the unit on the given quantity; this allows the unit to be cancelled. The unit in the numerator is the unit on the desired quantity.
  4. Insert numbers into the conversion factor. For a mole-to-mole problem, these will be the coefficients in the balanced chemical equation.
  5. Use your calculator to calculate the numerical value of the answer. Multiply the given value by the numerator and divide by the denominator.
 
 
 
 

Before You Leave

  • Download our Study Card on Mole-to-Mole Conversions. Save it to a safe location and use it as a review tool. 
  • Having troubles with using Conversion Factors. Study our Factor Label Method page. It discusses the method of using conversion factors to cancel units and solve for an unknown.
  • Problem Set ST2: Mole-to-Mole Stoichiometry at our Calculator Pad provides awesome practice as a follow-up to this Tutorial page. Your answers are immediately evaluated and feedback is given. You can correct your answers.
  • The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Consider Conversion Factors A and B below. They are each used in a mole-to-mole stoichiometry problem. For each, indicate the given quantity and the desired quantity.
 

Check Answer
 


 
2. Consider the balanced chemical equation for the single replacement reaction between aluminum and zinc chloride.
 
2 Al   +   3 ZnCl2   → 2 AlCl3  +   3 Zn
 
How many moles of AlCl3 are produced from the reaction of 11.8 moles of ZnCl2?

Check Answer



 
3. When an electric current is passed through a sample of water (electrolysis), the water decomposes into hydrogen and oxygen gas. The balanced chemical equation for the decomposition of water into its elements is
 
2 H2O   →   2 H2   +   O2
 
How many moles of H2 are produced from the decomposition of 6.52 moles of H2O?
 
Check Answer

 


 

Next Part of this Lesson: Mole-to-Mass Relationships

Jump to Next Lesson: Non-Stoichiometric Conditions

View: Chapter Contents