Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Relating Stoichiometric Quantities
Part d: Percent Yield
Part a: Mole-to-Mole Relationships
Part b: Mole-to-Mass Relationships
Part c: Mass-to-Mass Relationships
Part d: Percent Yield
Part e: Stoichiometry Plus
 Yield
Yield
Yield refers to the amount of product produced by a chemical reaction. It is most often expressed in grams. In Chemistry, we distinguish between theoretical yield and actual yield. Theoretical yield is the amount of product we would expect to be produced based on stoichiometry calculations and assuming all reactants react and turn to products. Actual yield is the amount of product actually recovered when an experimental trial is performed and the mass of product is measured. Actual yield is based on a measurement.
A student may perform an experiment to produce magnesium oxide by the combustion of magnesium.
2 Mg(s) + O2(g) → 2 MgO(s)
 Based on the mass of magnesium used in the experiment, the student might use stoichiometry to determine that 2.65 g of MgO should be produced. This is the theoretical yield; it is determined by a stoichiometric calculation using the mass of reactant. Upon performing the experiment, the student might measure the mass of MgO actually produced to be 2.12 g. This is the actual yield; it determined by performing the experiment and measuring the mass of the product. Generally, it is expected that the actual yield would be less than or (at best) equal to the theoretical yield.
Based on the mass of magnesium used in the experiment, the student might use stoichiometry to determine that 2.65 g of MgO should be produced. This is the theoretical yield; it is determined by a stoichiometric calculation using the mass of reactant. Upon performing the experiment, the student might measure the mass of MgO actually produced to be 2.12 g. This is the actual yield; it determined by performing the experiment and measuring the mass of the product. Generally, it is expected that the actual yield would be less than or (at best) equal to the theoretical yield.
Percent Yield
Chemists often rely upon a percent yield calculation to express how closely the actual yield comes to the theoretical yield. A percent yield value of 100% for an experimental trial indicates that all the product that could have been produced was indeed produced. The equation for calculating percent yield is …

Suppose an experimental trial is performed and the actual yield is determined by collecting and measuring the product amount after being careful to isolate it from other contaminants. The best-case scenario for such a trial would be a 100% yield. A 100% yield indicates that all that could be produced (theoretical yield) was indeed produced, collected, and measured (actual yield). A 100% yield is an ideal situation and is seldom realized in an experimental trial. Often times, side reactions cause other products to be produced rather than the target product that the lab group is attempting to measure. And often times, a reactant does not fully react and remains in unreacted form once the experimental trial is complete. These are just a couple of the many reasons why the actual yield is less than the theoretical yield.
Stoichiometry Problems with Percent Yield
Percent yield problems are relatively common in introductory Chemistry courses. Such problems require careful reading and reflection in order to distinguish between experimental values and theoretical values. And they usually require a stoichiometry calculation to relate the reactant amount to a theoretical amount of product. Here’s an example of such a problem.
Given: 2 Mg(s) + O2(g) → 2 MgO(s)
In an experiment, a lab group burns a 1.60-gram magnesium ribbon in an effort to produce magnesium oxide. If the group collects 2.12 g of MgO, then what is their percent yield?
The 1.60-gram value is the amount of Mg reacted in the experiment. It can be used with a stoichiometry calculation to determine the theoretical yield of MgO. This would be a straightforward
gram-to-gram stoichiometry calculation. The 2.12 g MgO value is the actual yield; it was determined by experiment. The percent yield (the desired quantity in the problem) can be calculated from the theoretical yield and the actual yield. We will complete this problem in Example 1.
The above problem is just an example of the many variations of problems that a Chemistry student might confront. The given quantities can vary from problem to problem. As a Chemistry student, you will need to …
- know and be able to use the percent yield equation,
- be able to distinguish between theoretical information (e.g., mass of reactant) and the actual yield when reading the problem, and
- (often times) be able to determine the theoretical yield by means of a stoichiometry calculation.
Example 1
Given: 2 Mg(s) + O2(g) → 2 MgO(s)
In an experiment, a lab group burns a 1.60-gram magnesium ribbon in an effort to produce magnesium oxide. If the group collects 2.12 g of MgO, then what is their percent yield?
We begin the solution by determining the theoretical yield of MgO from the mass of Mg that reacts. This is a three-step gram-to-gram stoichiometry conversion (as done in
Lesson 2c) that begins with 1.60 g of Mg. The molar mass of Mg, the coefficients from the balanced equation, and the molar mass of MgO will be needed to form the three conversions factors. Molar mass values can be determined using
a periodic table.
The conversion factor set up is done to cancel all units except for the mass of MgO in grams. We have used pairs of colored diagonal lines to show the unit cancellation. The resulting value will be the grams of MgO; this is the theoretical yield. The set-up is shown below.
Numerical values for molar mass of Mg, the coefficients (2 for both Mg and MgO), and the molar mass of MgO can be inserted into the conversion factors.
The percent error can be determined using the actual yield (given as 2.12 g MgO) and the theoretical yield (calculated as 2.65 g MgO).
Example 2
Given: 4 Al(s) + 3 O2(g) → 2 Al2O3(s)
In an experiment, a lab group burns 2.37 g of Al in an effort to produce aluminum oxide. If the group collects 3.36 g of Al2O3, then what is their percent yield?
The given quantity 2.37 g Al is the mass of a reactant. The theoretical yield can be determined by stoichiometry. A three-step conversion from the mass of reactant to the mass of Al
2O
3 would provide a value for the theoretical yield. The given quantity 3.36 g Al
2O
3 is the actual yield; it is the amount produced and collected when the experiment is performed. To calculate the percent yield, the theoretical yield must first be calculated. The method of calculating the mass of Al
2O
3 produced is the same method discussed in
Lesson 2c. There are three steps involved and thus three conversion factors. The molar masses of Al and Al
2O
3 are needed. They can be determined using
a periodic table.
The conversion factor set up (without units) is shown below. Note how the units cancel. The one unit that does not cancel is the grams of Al
2O
3. This would be the theoretical yield.
The numbers for molar mass and the coefficients (4 for Al and 2 for Al
2O
3) can be inserted into the conversion factors. The results is calculated in the usual manner. (See
Lesson 2c for all the details.)
The actual yield (given as 3.36 g Al
2O
3) and the theoretical yield (calculated as 4.48 g Al
2O
3) can be used to calculate the percent yield.
Example 3
Given: N2(g) + 3 H2(g) → 2 NH3(g)
The above reaction is known to operate with a 65.0% yield. What mass of reactants - N2 and H2 - are required to produce 1.00 kg of product?
The actual yield in this problem is 1.00 kg. This is the amount that is actually produced. The value is equivalent to 1.00x10
3 grams. Since the percent yield is 65.0%, the theoretical yield must be greater than 1.00 kg. The theoretical yield can be calculated using the percent yield equation. The work is shown below. (T=theoretical yield)
The theoretical yield is 1.54x10
3 grams. This is the theoretical yield of NH
3. The value can be used to determine the mass of N
2 and of H
2 that are required. This involves two three-step stoichiometry problems. The un-rounded version of 1.54x10
3 grams will be used in the calculations. The molar masses of N
2, H
2, and NH
3 will be needed. The values can be determined using
a periodic table.
Each of the two conversions will involve three steps. The goal of the steps is to cancel units and arrive with the grams of N
2 and the grams of H
2. We will begin with the N
2 calculation. The conversion factor set-up is shown below.
Numerical values for the molar masses and the coefficients can be inserted into the conversion factors. The mass of N
2 required to produce 1.00-kg of NH
3 at 65.0% yield can be calculated. The resulting answer is rounded to
the proper number of significant digits.
The same process can be repeated for H
2. The conversion factor set up is …
The amount of H
2 required to produce 1.00-kg of NH
3 at 65.0% yield can be determined after inserting the molar mass values and the coefficients into the equation. The resulting answer is rounded to
the proper number of significant digits.
Before You Leave
- Download our Study Card on Percent Yield. Save it to a safe location and use it as a review tool.
- The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the
Check Answer buttons when ready.
1. Suppose the mass of a reactant used in an experiment is known.
- Can the actual yield be determined?
- Can the theoretical yield be determined?
- Can the percent yield be determined?
2. Use your understanding of theoretical yield, actual yield, and percent yield to complete the following table.
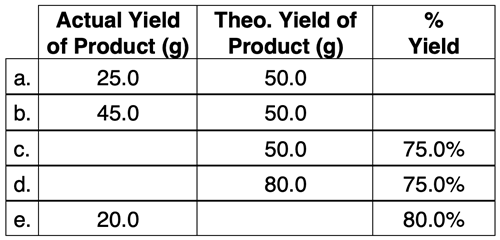
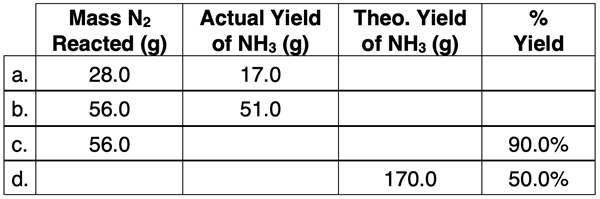
3. Given the reaction: N
2(g) + 3 H
2(g)
→ 2 NH
3(g)
Use your understanding of stoichiometry, theoretical yield, actual yield, and percent yield to complete the following table.
4. Given: 4 Al(s) + 3 O
2(g)
→ 2 Al
2O
3(s)
In an experiment, a lab group burns 1.02 g of Al in an effort to produce aluminum oxide. If the group collects 1.58 g of Al
2O
3, then what is their percent yield?