Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Chemical Reactions and Enthalpy Change
Part b: Hess's Law
Part a:
Enthalpy Change
Part b: Hess's Law
Part c:
Heat of Formation
Part d:
Bond Enthalpy and ∆H
Part e:
Thermal Stoichiometry
The BIG 3 of Thermochemical Equations
We introduced thermochemical equation in Lesson 2a. They are balanced chemical equations that are accompanied by information about the enthalpy change for the reaction as stated. Here’s two versions of thermochemical equations for the combustion of methane.
CH4(g) + 2 O2(g) → 2 H2O(l) + CO2(g) ∆H = -890 kJ
CH4(g) + 2 O2(g) → 2 H2O(l) + CO2(g) + 890 kJ
In the first version, the enthalpy change is listed as a ∆H value to the right of the equation. In the second version, the enthalpy change is added into the equation as a heat term. The heat term is a reactant for endothermic reactions and a product for exothermic reactions.
In this part of Lesson 2, we will learn three rules regarding thermochemical equations and learn how to use them to determine the enthalpy change of chemical reactions. The three rules are:
- The ∆H is directly proportional to the amount of reactants and products.
We have referred to enthalpy change as a stoichiometric quantity. The kJ of heat absorbed or released by a specific reaction is dependent on how much reactant or product is involved. It can be expressed as a ratio. For the methane combustion reaction (above), the ratio is -890 kJ/1 mol CH4 or -890 kJ/2 mol O2. If the coefficients of the balanced equation are doubled or halved, the ∆H value will double or halve.
- The ∆H value for a reaction is equal and opposite to the ∆H value for the reverse reaction.
The synthesis of liquid water from its elements is exothermic and has a ∆H value of -286 kJ/mol. The reverse process - the decomposition of water into its elements - is endothermic and has a ∆H of +286 kJ/mol. This is illustrated by the two thermochemical equations below.
H2(g) + ½ O2(g) → H2O(l) ∆H = -286 kJ
H2O(l) → H2(g) + ½ O2(g) ∆H = +286 kJ
 The ∆H value for a reaction is independent of how many steps are taken between reactants and products.
The ∆H value for a reaction is independent of how many steps are taken between reactants and products.
This ↑↑↑↑↑. This is the topic of Lesson 2b. Understanding this third rule and being able to apply it with Rules 1 and 2 is the goal of Lesson 2b. This third rule suggests that enthalpy is a state function. That will take some explaining. Read on!
Enthalpy as a State Function
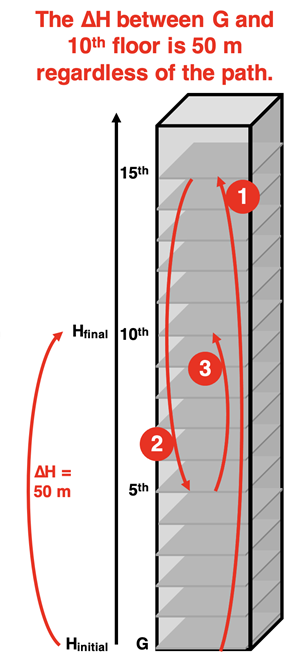
Altitude is a property that we refer to as a
state function. While it has little to do with Chemistry, it is a useful property for explaining the idea of a state function. Suppose that you are in a very tall building with an elevator that has floors positioned 5-meters apart. You start on Ground level - an altitude of 0 meters. You ride the elevator up to the 10
th floor at an altitude of 50 meters. Here’s an easy question - by how much did your altitude change? Easy answer - 50 meters.
Now suppose you start at Ground level and ride the elevator to the 15
th floor, down to the 5
th floor, and finally back up to the 10
th floor. You’ve reached the final destination. The ride ends. What is your altitude change? It’s a bit more difficult question. But the answer is still 50 meters. In the initial state, you had an altitude of 0 meters. In the final state you had an altitude of 50 meters. The change in altitude is still 50 meters.
This illustrates the concept of a state function. A change in its value from the initial to the final state is not dependent upon the path. The altitude change only depends upon the two states - the altitude at Ground floor and the altitude on the 10
th floor. The change in altitude for a trip from the Ground floor to the 10
th floor is always 50 meters no matter how you get there. Altitude is a path-independent quantity. This makes it a state function.
Many chemical properties are what we refer to as state functions. Enthalpy is a state function. As we have discussed, reactants have a certain amount of enthalpy. Products have a different amount of enthalpy. If generic reactants A and B change into generic products C and D, then the enthalpy change is simply the difference between the enthalpy of products and the enthalpy of reactants.
∆H = Hproducts - Hreactants
And more importantly, because enthalpy is a state function, the enthalpy change will be the same no matter how the overall change occurs. The change could occur in one step, two steps, three steps, or more steps. But however it does occur, the change in enthalpy will not be affected by the pathway or number of steps.
Just as there are many ways to use an elevator and get from the Ground floor to the 10
th floor, there are many ways to get from reactants A + B to products C + D. And no matter how one gets from the intial state (reactants) to the final state (products), the enthalpy change will be the same because enthalpy is a state function.
Hess’s Law of Constant Heat Summation
Hess’s Law of Constant Heat Summation, more affectionately known as
Hess’s Law, states that the enthalpy change for a multi-step process is the sum of the enthalpy change of the individual steps. The diagram below illustrates this idea for the generic reaction of A + B → C + D:
Observe how the enthalpy change between the initial state (the reactants A + B) and the final state (the products C + D) is -400 kJ regardless of the number of steps. Also observe how the enthalpy change for the overall process is the sum of the enthalpy changes of the individuals steps in the process.
The Art of Adding Reactions

We’re getting close to being equipped to accomplish our goal - using the three rules of thermochemical equations to determine the enthalpy change of a reaction. There’s one more skill that you will need - the skill of adding reactions together to obtain an overall target reaction. The typical Hess’s law problem will provide two or three reactions with given ∆H values. The problem will require that you arrange and “add the equations together” to achieve the
Target Equation and to determine the ∆H of the
Target Equation. An example of such a problem is shown at the right.
The concept of adding chemical equations is a difficult one for many students. For those who have added algebraic equations in math with formulas including x, y, and z (or the like), it may help to think about that process since adding chemical equations works the same way. (And for those who have not done this in math or regret having done it in math, forget the previous sentence.)
When you add equations in chemistry, you are adding all the reactants together with their coefficients and all the products together with their coefficients. Consider Equations 1 and 2 below.
Equation 1: J + 3M → 2L + N
Equation 2: 3J + 2L → 2M + N
The sum of these two equations leads to Equation 3:
Equation 3: J + 3M + 3J + 2L → 2L + N + 2M + N
Note how both original equations had two reactants each and two products each. So, the sum of the two equations has four reactants and four products as expected.
Once the two (or more) equations are added, you will need to
cancel and group formulae. Formulae (plural for formula) will cancel if the same amount of that formula is present on opposite sides of the chemical equation (the
summed one). In the above example (Equation 3), the 2L will cancel since it is present on both the reactant and product side. Formulae will partially cancel if there are unequal amounts of that formula present on opposite sides of the chemical equation. For instance, there are 3M on the reactant side and 2M on the product side; this will result in partial cancellation. 2M can be cancelled from each side, leaving 1M on the reactant side. The equation becomes three formulas shorter.
Equation 3 (shortened): J + M + 3J → N + N
Grouping formulas means that if there are two instances of a formula on the same side of the equation, then they can be added together. For instance, there is a J and a 3J on the reactant side of the above equation. Those would add to 4J. And similarly, there is an N and a second N on the product side. Those would add to 2N. Implementing these two groupings would simplify the chemical equation to three terms:
Equation 3 (very shortened): M + 4J → 2N
And if you’re wondering, it doesn't matter the order in which you write these reactants as long as you keep them as reactants. You can write 4J + M if you like. The same is true for the products.

In our J-L-M-N example, you were given the equations to add. In a typical Hess’s Law problem, you will be given equations but will have to decide how to manipulate them (reverse one, multiply another by two, etc.) in order for them to add up to yield the Target Equation. The task of arranging and adding the equations so as to achieve the Target Equation is the more difficult task. It is a type of task that is
better caught than taught. In other words, you will need to see several worked-out examples and try some on your own. You must be patient with the process of arranging and adding. There is no single way to solve this problem of adding two equations to arrive at the Target Equations. It is a process that requires trial and error. Commit to patiently working the process.
Let’s begin with our first example -
the problem listed above. As we proceed through the solution, we will depend upon these four steps. While the process will always involve trial-and-error, these steps will efficiently guide each iteration of the trial-and-error process.
Example 1
If given the thermochemical equations …
Equation 1: N
2(g) + O
2(g) → 2 NO
(g) ∆H = +182 kJ
Equation 2: N
2(g) + 2 O
2(g) → 2 NO
2(g) ∆H = +66 kJ
Determine the ∆H of the
Target Equation:
Target Eq’n: 2 NO
2(g) → 2 NO
(g) + O
2(g) ∆H = ??
Solution:
Step 1: Manipulate the Given Equations
We want to begin by manipulating and adding Equations 1 and 2 in order to achieve the Target Equation. Remember the first two rules of thermochemical equations - they involve multiplying an equation through by a coefficient and reversing and equation. This is how you will “manipulate” the equations before adding them.
Notice that the target Equation 2 has NO
2(g) on the reactant side. Only Equation 2 has NO
2 in it. But because NO
2 is on the product side of Equation 2, we will reverse Equation 2. When we do reverse it, we will have to change the sign on ∆H from + to -.
Equation 1: N
2(g) + O
2(g) → 2 NO
(g) ∆H = +182 kJ
Equation 2 (reversed): 2 NO
2(g) → N
2(g) + 2 O
2(g) ∆H = -66 kJ
Step 2: Add the Manipulated Versions of the Given Equations
Now we will add Equations 1 and 2 to get Equation 3 below:
Equation 3: N
2(g) + O
2(g) +
2 NO2(g) →
2 NO(g) + N
2(g) + 2 O
2(g)
Observe how Equation 3 has two of the formulas we need in our Target Equation -
2 NO2(g) on the reactant side and
2 NO(g) on the product side. That means we’re getting close to the Target Equation.
Step 3: Cancel and Group Formulae
Now we need to do some Cancelling and Grouping. There are the same number of N
2(g) on reactant and product side of Equation 3. They will cancel. Equation 3 becomes:
Equation 3 (shortened): O
2(g) + 2 NO
2(g) → 2 NO
(g) + 2 O
2(g)
And there is one O
2(g) on the reactant side and two O
2(g) on the product side. We can cancel one O
2(g) from each side, leading to a more shortened version:
Equation 3 (very shortened): 2 NO
2(g) → 2 NO
(g) + O
2(g)
Eureka! Equation 3 is now identical to the Target Equation.
Let’s review what was done:
First, we manipulated Equation 2, reversing it so as to get the 2 NO
2(g) formula on the reactant side. Second, we added the two equations together. Third, we did some Cancelling and Grouping and were fortunate enough to have produced the Target Equation as a result.
Step 4: Use Hess’s Law to Calculate the ∆H
Our fourth and final step can now be done - use Hess’s Law to calculate ∆H of the Target Equation.
We produced the Target Equation by adding Equation 1 (as is) and a reversed form of Equation 2. So, we will need to add the ∆H of Equation 1 to the ∆H of the reversed form of Equation 2.
∆HTarget Equation = ∆HEquation 1 + ∆H Equation 2 (reversed)
∆HTarget Equation = +182 kJ + (-66 kJ)
∆HTarget Equation = +116 kJ
Our four-step process, combined with Hess’s Law, has led to the following thermochemical equation:
2 NO2(g) → 2 NO(g) + O2(g) ∆H = +116 kJ
We have two more worked-out examples. We recommend that you attempt them on your own using these four steps as a guide to your trial-and-error solution. Then tap on the
View Answer button to check your answer or to view the complete solution.
Example 2
If given the thermochemical equations …
Equation 1: 2 NO
(g) + O
2(g) → 2 NO
2(g) ∆H = -116 kJ
Equation 2: N
2O
4(g) → 2 NO
2(g) ∆H = +55 kJ
Determine the ∆H of the
Target Equation:
Target Eq’n: 2 NO
2(g) + O
2(g) → N
2O
4(g) ∆H = ??
Example 3
If given the thermochemical equations …
Equation 1: N
2(g) + 3 H
2(g) → 2 NH
3(g) ∆H = -92 kJ
Equation 2: 2 H
2(g) + O
2(g) → 2 H
2O
(l) ∆H = -572 kJ
Equation 3: N
2(g) + 2 O
2(g) → 2 NO
2(g) ∆H = +66 kJ
Determine the ∆H of the
target equation:
Target Eq’n: 2 NH
3(g) + 4 H
2O
(l) → 2 NO
2(g) + 7 H
2(g) ∆H = ??
Some Final Tips
We will leave you with three tips for making smoother work of using Hess’s Law to solve problems. Then it is time for you to practice.
- Observe. Inspect. Gather Information.
Don't stall just because you don't know what to do. Instead, look at and compare the given equations and the target equation. Pay attention to details. Ask and answer ... What formula (if any) is present in only one of the given equations and shows up in the Target Equation? How do the coefficients in the given equation and the Target Equation compare for this formula? And what formulas are present in both of the given equations but doesn't show up in the Target Equations. For this formula, how do the coefficients in the given equations compare to each other? After you have gathered this information, you will be ready for the next two strategies.
- Look for a Formula Present in only One of the Given Equations
A formula that is present in only one of the given equations will show up in the Target Equation. This is an important starting point. If the formula is a reactant in the given equation but a product in the Target Equation, then you know for certain that the given equation will have to be reversed. And if the coefficients are different, then you also know that a multiplier will have to be used so that the coefficients are the same in both the manipulated version of the given equation and the Target Equation. Make the needed adjustments based on this observation. Often times doing so will be all you need to do before adding the given equations. If you need to do more then proceed to the next strategy ...
- Look for a Formula Present in Both of the Given Equations and Absent in the Target Equation
A formula that is present in both of the given equations but absent in the Target Equation is a formula that has cancelled. The only way that such a formula can cancel when added is if the formula is a reactant in one of the given equations and a product in the other given equation ... and if they have the same coefficient. This suggests two possible manipulations: First, one of the two given equations may have to be reversed so that the formula in focus is a reactant in one equation and a product in the other equation. And second, one of the equations may need a multiplier in order for the coefficient in front of the formula to be the same coefficient in both given equations. Make the needed adjustments based on this observation. Often times doing so will be all you need to do before adding the given equations.
Before You Leave
- Download our Study Card on Hess’s Law. Save it to a safe location and use it as a review tool. (Coming Soon.)
- Our Hess’s Law Concept Builder may be the best practice ever for manipulating and adding the given equations to form the Target Equation. You have to at least try it.
- Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Thermal Chemistry page. Try Problem Set TC11: Hess’s Law for more practice.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. Use the first two rules of thermochemical equations to answer the following questions:
- Given: N2(g) + 3 H2(g) → 2 NH3(g) ∆H = -92 kJ,
what is the ∆H of 3 N2(g) + 9 H2(g) → 6 NH3(g)?
- Given: N2(g) + 3 H2(g) → 2 NH3(g) ∆H = -92 kJ,
what is the ∆H of 2 NH3(g) → N2(g) + 3 H2(g)?
- Given: N2(g) + 3 H2(g) → 2 NH3(g) ∆H = -92 kJ,
what is the ∆H of 4 NH3(g) → 2 N2(g) + 6 H2(g)?
- Given: N2(g) + 3 H2(g) → 2 NH3(g) ∆H = -92 kJ,
what is the ∆H of 10 NH3(g) → 5 N2(g) + 15 H2(g)?
2. Which of the following statements are true of a quantity that is a state function? Select all that are true.
- The value of the quantity is always the same.
- A change in the quantity between two different states will not depend upon how many steps were taken between those states.
- The value of the quantity depends upon the properties of a particular state and not on how the state was reached.
- The quantity is a path-dependent quantity.
- A change in the quantity will depend upon how many steps are taken from the initial value to the final value.
3. Consider:
A + B → C ∆H = -800 kJ
The proccess is carried out in two steps as shown with D being an
intermediate.
Step 1: A → D ∆H = +200 kJ
Step 2: B + D → C ∆H = ???? kJ
What is ∆H of step 2?
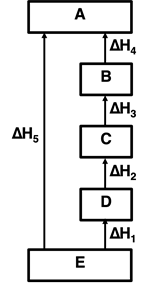
4. Consider the enthalpy diagram at the right for E changing to A, directly and by means of four individual steps. Given that ...
ΔH
1 = 50 kJ,
ΔH
2 = 75 kJ,
ΔH
4 = 150 kJ, and
ΔH
5 = 375 kJ,
... determine the value of ΔH
3?
5. On Planet Exwizee, where the main elements are X, Y, and Z, it is known that compounds of elements X, Y, and Z will react in the following ways:
Equation 1: Y + X
2Z → XY + XZ
Equation 2: 2 X
2Z → X
2 + 2 XZ
The enthalpy changes for these two reactions are ...
∆H
1 = +208 kJ
∆H
2 = -173 kJ.
Use this information to determine the enthalpy change (∆H) of the Target Equation …
X
2 + 2 Y → 2 XY
6. Consider these balanced chemical equations and their corresponding enthalpy change values:
Equation 1: P
4(s) + 10 Cl
2(g) → 4 PCl
5(g) ∆H = -7736 kJ
Equation 2: PCl
3(g) + Cl
2(g) → PCl
5(g) ∆H = -562 kJ
Use this information and Hess's law to determine the enthalpy change for this Target Equation:
P
4(s) + 6 Cl
2(g) → 4 PCl
3(g)