Lesson 2: Chemical Reactions and Enthalpy Change

Part a: Enthalpy Change

Part a: Enthalpy Change
Part b: Hess's Law
Part c: Heat of Formation
Part d: Bond Enthalpy and ∆H
Part e: Thermal Stoichiometry

 
 

What is Enthalpy Change?

In Lesson 1, we learned that energy flows out of or into a reaction system in the form of heat during a reaction. This occurs because reactions are accompanied by a change in chemical potential energy. Chemists use a quantity known as enthalpy (abbreviated H) to describe reaction systems. Enthalpy accounts for the total energy of the reaction system - the potential energy associated with particle interactions, the kinetic energy associated with particle movement, and the energy required to make room for the system in the surroundings (often referred to as P•V).
 
Enthalpy is indeed a technical term … but what you really need to know is this: When a reaction is performed at a constant pressure (the usual condition), the quantity of heat exchanged between the system and surroundings is equal to the change in enthalpy (∆H).

Q = ∆H (at constant pressure)

By using calorimetry methods, we can determine the enthalpy change (assuming the usual condition of there being a constant pressure). This change in enthalpy is related to changes in energy within the system.
 
The ∆H value can be positive or negative depending on whether the enthalpy of reactants is lower or higher than that of products. When the enthalpy of reactants is higher than the enthalpy of products, the reaction system has a negative enthalpy change; heat is released by the system to the surroundings. On the other hand, if products are higher in enthalpy than the reactants, there is a positive enthalpy change and heat is absorbed by the reaction system.

 
 

 
 
 

Enthalpy Level Diagrams

If you’re arriving at this page from Lesson 1 (particularly Lesson 1c), then you will likely observe that we are visiting some earlier ideas and giving a new name to them. The term enthalpy is replacing what we have earlier described as energy. Enthalpy is a form of energy. We can represent reactions with enthalpy level diagrams, similar to how we used energy level diagrams.
 
Exothermic reactions release heat from the system to the surroundings. For such reactions, the enthalpy level of reactants is greater than that of products. This is shown on the left below. Endothermic reactions in which heat is absorbed by the system from the surroundings would display a higher enthalpy level for the products. This is shown on the right below.
 

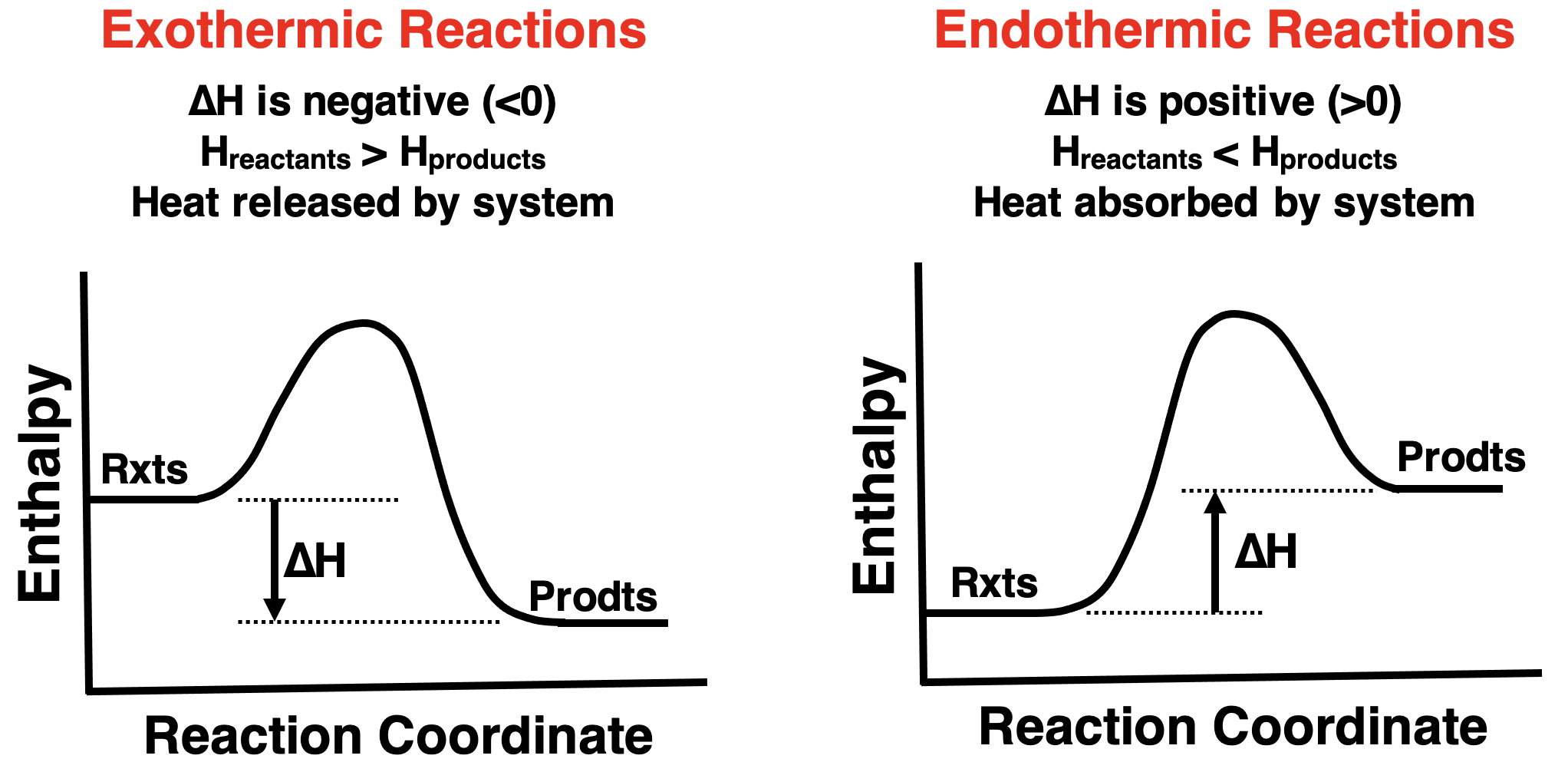
 “Reaction Coordinate” is a generic term that provides a measure of the reaction’s progress from its initial state (reactants) to its final state (products).

 

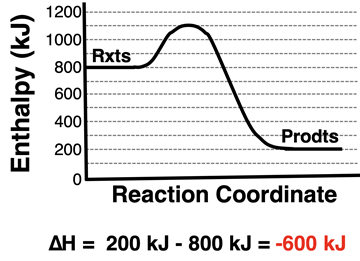
If coordinate values are provided for the vertical axis, an enthalpy change value can be determined from the graph. It is simply the difference between the enthalpy of the products and that of the reactants. Values for the enthalpy of products and reactants can be read off the axis. The ∆H value is calculated as
 

∆H = H_products - H_reactants

 
 

 

Thermochemical Equations

Every chemical reaction has a unique enthalpy change or ∆H value. The enthalpy change is dependent on how much of the reactants are involved in the reaction. For instance, the enthalpy change associated with the combustion of 1 mole of methane gas (CH₄) is approximately -890 kJ. When two moles of methane undergo combustion, 1780 kJ of energy are released. And 445 kJ of energy is released when 0.5 mole of methane is burned. In this sense, enthalpy change is a stoichiometric quantity. It is a how much quantity that can be related to the amount of reactants and products involved in the reaction.
 
A thermochemical equation is a balanced chemical equation that displays enthalpy change information about the reaction. The information can be displayed by listing a ∆H term beside the balanced equation. The thermochemical equation for the combustion of methane gas is …

CH₄(g)  +  2 O₂(g)  →  2 H₂O(l)  +  CO₂(g)   ∆H = -890 kJ

The value of ∆H must be consistent with the coefficients in the balanced chemical equation. The above equation indicates that the enthalpy change is -890 kJ when 1 mole of CH₄ gas reacts with two moles of O₂ gas. Since enthalpy change is a stoichiometric quantity, the value doubles for the combustion of twice as much methane and halves for the combustion of one-half as much methane.

2 CH₄(g)  +  4 O₂(g)  →  4 H₂O(l)  +  2 CO₂(g)   ∆H = -1780 kJ
 
½ CH₄(g)  +  O₂(g)  →  H₂O(l)  +  ½ CO₂(g)   ∆H = -445 kJ

 

The enthalpy change information can also be communicated by including a heat term within the balanced chemical equation. The side of the equation - reactant side or product side - to which it is added matters. Methane combustion is an exothermic reaction. Heat is released or produced by the reaction. Heat is a product and the heat term is added to the product side.

CH₄(g)  +  2 O₂(g)  →  2 H₂O(l)  +  CO₂(g)  +   890 kJ

And of course, if the coefficients are changed, so does the value of the heat term. This emphasizes that enthalpy is a stoichiometric quantity.

2 CH₄(g)  +  4 O₂(g)  →  4 H₂O(l)  +  2 CO₂(g)  +  1780 kJ
 
½ CH₄(g)  +  O₂(g)  →  H₂O(l)  +  ½ CO₂(g)  +  445 kJ

 

For endothermic reactions, heat is absorbed by the reaction system. The reaction requires energy input from the surroundings. Heat acts as a reactant in endothermic reactions and the heat term is placed on the reactant side. The decomposition of water into its elements is an endothermic reaction with a ∆H value of +286 kJ per mole of water. Emphasis again must be placed on the stoichiometric nature of this ∆H value. It is listed as 286 kJ per one mole of H₂O. When writing the thermochemical equation or including the heat term in the equation, the coefficients, the ∆H value, and the heat term must agree with 286 kJ per one mole of H₂O. This is demonstrated below.

H₂O(l)  →  H₂(g)  +  ½ O₂(g)   ∆H = +286 kJ
 
2 H₂O(l)  →  2 H₂(g)  +  O₂(g)   ∆H = +572 kJ
 
H₂O(l)  +  286 kJ  →  H₂(g)  +  ½ O₂(g)
 
2 H₂O(l)  +  572 kJ  →  2 H₂(g)  +  O₂(g)

 

 
 
 

Why is there an Addition Symbol?

Many beginning students of Chemistry are troubled by the fact that exothermic reactions like the combustion of methane have negative ∆H values but the heat term has an addition (plus sign) symbol in front of it when included as a product. Such students often want to subtract the term from the product side since the ∆H has a “-” in front of the value. 

 

 
There’s likely a lot of factors underlying this confusion. First, when we state ∆H = -890 kJ, the negative means less than 0 and is no way associated with the subtraction symbol. A less than 0 value (that is, a negative number) should never be associated with a subtraction process. Second, when we write any balanced chemical equation, we always use the “+” symbol to communicate “and”.  For brevity sake, we might read “CH₄  +  2 O₂  →  ” as “methane plus 2 oxygen”. But what we really mean is “1 mole of methane and 2 moles of oxygen react to produce …”. And if ever saw a “-” symbol in the equation, we would likely be very bothered by it. The heat term is always added. The less than 0 symbol (“-”) on ∆H will indicate the side to which the heat term is added. The heat term is added to the product side when ∆H is negative. The following summary may help:

 
 
 

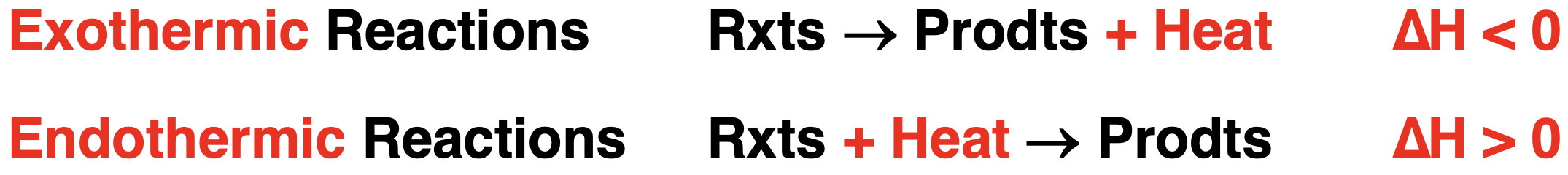
Heat of …

In Lesson 1d, we introduced two new terms - heat of fusion and heat of vaporization. These types of data fall under the generic category of heat of reaction The heat of reaction is the heat released (or absorbed) by the reaction system under constant pressure conditions. It is the enthalpy change for a reaction. Other examples include heat of sublimation, heat of combustion, heat of solution, heat of formation, and heat of decomposition.
 
Heat of reaction values are always stated as kJ per mole values. The word that comes after heat of provides a description of the type of reaction or state change that the ∆H value pertains to. So, a heat of solution value describes the enthalpy change for dissolving 1 mole of a substance (usually in water). The heat of combustion value describes the enthalpy change for burning 1 mole of a substance. The heat of decomposition describes the enthalpy change for the decomposition of 1 mole of a substance.
 
It is important to recognize the significance of heat of reaction values being per mole quantities. The heat of combustion of methanol is -726 kJ/mol. The value indicates the combustion reaction of 1 mole of methanol (CH₃OH) has an enthalpy change of -726 kJ. The negative sign indicates that the reaction is exothermic. We could write:

CH₃OH(l)  +  ³/₂ O₂(g)  →  2 H₂O(l)  +  CO₂(g)   ∆H = -726 kJ
 
or
 
CH₃OH(l)  +  ³/₂ O₂(g)  →  2 H₂O(l)  +  CO₂(g)  + 726 kJ

 
The fractional coefficient in front of O₂ on the reactant side is typically removed by multiplying all coefficients in the equation by 2. Doing so would mean that the ∆H value and the heat term would also have to be doubled. The result is
 

2 CH₃OH(l)  +  3 O₂(g)  →  4 H₂O(l)  +  2 CO₂(g)   ∆H = -1452 kJ
 
2 CH₃OH(l)  +  3 O₂(g)  →  4 H₂O(l)  +  2 CO₂(g)  + 1452 kJ

 
While the doubling process changes the ∆H value, it doesn’t change the heat of combustion value. The heat of combustion is just displayed as being -1452 kJ per 2 moles … which is equivalent to -726 kJ per 1 mole. Heat of reaction values are always stated on a per mole basis.

 

 
 
 

Determining ∆H Experimentally

Enthalpy change values for chemical reactions can be determined using calorimetry methods. A typical chemistry course will include one or more labs in which a coffee cup calorimeter is used to determine an enthalpy change. Because chemical reactions in labs occur at constant pressure (the pressure of the room), the enthalpy change is related to the heat released or absorbed by the system. Measuring the temperature change of the water in the cup allows one to determine the quantity of heat (Q) exchanged between the reaction system and the surroundings. And determining the amount of a reactant that reacted allows one to determine the number of moles (n) that reacted. Once Q and n are determined, the heat of reaction (∆H) can be expressed on a kJ per mole basis by dividing Q by n. The following two examples demonstrate the process.
(Visit Lesson 1d if you need to review calorimetry.)
 
 
 

Example 1

A large paraffin candle has a mass of 96.83 gram. A metal cup with 100.0 mL of water at 16.2°C absorbs the heat from the burning candle and increases its temperature to 35.7°C. Once the burning is ceased, the paraffin had a mass of 96.14 gram. Determine the heat of combustion of paraffin in kJ/mole. GIVEN: density of water = 1.0 g/mL; molar mass of paraffin is 352 g/mol.
 
Solution:
The first step involves using Q = m•C•∆T to determine the heat released by the reaction.
 
Given:  m_water = 100.0 g,  C_water = 4.184 J/g/°C, T_initial = 16.2°C, T_final = 35.7°C.
Determine: Q = ???
 
Begin by determining the ∆T value of the water:
 
∆T = T_final - T_initial = 35.7°C - 16.2°C = 19.5°C
 
Now use the Q equation to determine the heat absorbed by the burning of the paraffin:
 
Q_water = (100.0 g)•(4.184 J/g/°C)•(19.5°C) = 8158.8 J
Q_water = 8.16 kJ (rounded from 8.1588 kJ)
 
Since the water gained energy (increased temperature), the chemical system lost energy. The reaction is exothermic and is a negative value. The ∆H of the reaction is thus -8.16 kJ. But this must now be scaled to a per mole quantity. The mass of paraffin burned can be determined from the initial and final mass of the candle:
 
m_paraffin = 96.83 g - 96.14 g = 0.69 g
 
The moles of paraffin undergoing combustion can be determined by dividing the mass that was burned by the molar mass (given as 352 g/mol):
 
n_paraffin = 0.69 g • (1 mole/352 g) = 0.020 mol (rounded from 0.01960227 … mol)
 
To determine the heat of combustion in kJ/mol, the enthalpy change can be divided by the moles of paraffin reacted: Unrounded numbers are used in the calculation.
 
Heat of Combustion = -8.1588 kJ / 0.01960227 … mol
Heat of Combustion = -4200 kJ/mol
(rounded from -4162.17 … to two significant digits)
 
 
 

Example 2

A chemistry student dissolves 4.51 grams of sodium hydroxide (NaOH) in 100.0 mL of water at 19.5°C (in a calorimeter cup). As the sodium hydroxide dissolves, the temperature of the surrounding water increases to 31.7°C. Determine the heat of solution of the sodium hydroxide in kJ/mol.
 
Solution:
The first step involves using Q = m•C•∆T to determine the heat released by the reaction.
 
Given:  m_water = 100.0 g,  C_water = 4.184 J/g/°C, T_initial = 19.5°C, T_final = 31.7°C.
Determine: Q = ???
 
Begin by determining the ∆T value of the water:
 
∆T = T_final - T_initial = 31.7°C - 19.5°C = 12.2°C
 
Now use the Q equation to determine the heat released by the dissolving of the NaOH:
 
Q_water = (100.0 g)•(4.184 J/g/°C)•(12.2°C) = 5104.48 J
Q_water = 5.10 kJ (rounded from 5.10448 kJ)
 
The reaction is exothermic (the water temperature increased) and the ∆H is a negative value. The ∆H of the reaction is thus -5.10 kJ (rounded from -5.10448 kJ). But this must now be scaled to a per mole quantity. The moles of NaOH dissolved can be determine from the mass that was dissolved: The molar mass of NaOH is 39.9971 g/mol (determined using a periodic table).
n = 4.51 g • (1 mol / 39.9971 g)
n = 0.113 mol (rounded from 0.112758 … mol)
 
To determine the heat of solution in kJ/mol, the enthalpy change can be divided by the moles of NaOH dissolved. Unrounded numbers are used in the calculation.
 
Heat of Solution = 5.10448 kJ / 0.112758 … mol
Heat of Solution = -45.3 kJ/mol
(rounded from -45.269267 … kJ/mol)
 
 
 

Before You Leave

• Download our Study Card on Enthalpy Change. Save it to a safe location and use it as a review tool. (Coming Soon.)
• Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Thermal Chemistry page. Check out the Enthalpy Change problem set.
• Try our Enthalpy Change Concept Builder. Use calorimetry data and the amount of reactant to determine the enthalpy change for a stated reaction.
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Under what condition is the enthalpy change for a process equal to the quantity of heat that is exchanged between the system and the surroundings?

 
 

2. For each of the following statements, identify the reaction as being endothermic or exothermic.

1. Heat is transferred from the surroundings to the system. 
   
   Check Answer
   Answer:  Endothermic
   
   Energy enters the system - that's endo or into.
   
    
   
    
2. The temperature of the surroundings increases. 
   
   Check Answer
   Answer:  Exothermic
   
   Energy exits the system and warms up the surroundings.
   
    
   
    
3. The change in enthalpy is -200 kJ. 
   
   Check Answer
   Answer:  Exothermic
   
   Energy exits the system to the surroundings; this is what causes the decrease in enthalpy and the negative ∆H.
   
    
   
    
4. The enthalpy of products is greater than the enthalpy of reactants. 
   
   Check Answer
   Answer:  Endothermic
   
   Energy enters the system; this is what causes the enthalpy of the products to be greater than that of the reactants.
   
    
   
    
5. Heat is released to the surroundings by the system. 
   
   Check Answer
   Answer:  Exothermic
   
   Energy exits the system to the surroundings. "Exo" for exit.
   
    
   
    
6. The reaction is a combustion reaction. 
   
   Check Answer
   Answer:  Exothermic
   
   All true, combustion or burning reactions are exothermic. Energy is released by the system in the form of heat and/or light.
   
    
   
    
7. On a system diagram, the arrow extends from the surroundings into the system. 
   
   Check Answer
   Answer:  Endothermic
   
   The arrow represents the direction that heat flows. If it is shown as directed from surroundings to system, then the energy is going into the system. That's "endo" for into.
   
    
   
    
8. On an enthalpy level diagram, the reactants are at 600 kJ and the products are at 100 kJ. 
   
   Check Answer
   Answer:  Exothermic
   
   This describes a drop in enthalpy or a ∆H that is negative. This is characteristic of all exothermic reactions.
   
    
   
    
9. The ∆H value is positive. 
   
   Check Answer
   Answer:  Endothermic
   
   Energy is going into the system. This is what causes the final state (products) to be of a higher enthapy than the initial state (reactants).
   
    
   
    
10. The heat term is added to the product side in the thermochemical equation. 
    
    Check Answer
    Answer:  Exothermic
    
    Heat is a product; it is produced or released by the reaction system. This means energy is going out of the system to the surroundings.
    
     
    
     

 

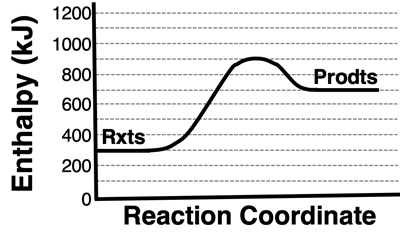
3. Consider the enthalpy level diagram at the right. The enthalpy change for this reaction is ____ kJ.

1. + 300
2. +400
3. +600
4. +700
5. +900
6. -200
7. -400
8. -600

 
 
​
4. What is meant by saying that “enthalpy change is a stoichiometric quantity”?


 
 
​
5. The thermochemical equation for the combustion of propane gas is ...
   
What is the enthalpy change for the following reaction? Include the proper +/- sign.
   


 
 
​
6. The heat of reaction for the synthesis of ammonia (NH₃) from nitrogen and hydrogen gas is approximately -46 kJ/mol. Write and balance a thermochemical equation for this reaction. Use the lowest whole number coefficients in the equation and add the heat term to the equation on the proper side.


 
 
​
7. The heat of combustion of butane is -2877 kJ/mol. Write and balance a thermochemical equation for the combustion of butane. Use the lowest whole number coefficients in the equation.


 
 
​
8. Jill Innout and Koo Lindown are conducting a lab to determine the heat of solution of ammonium nitrate (NH₄NO₃). They measure out 4.00 g of the solid and dissolve it in 50.0 mL of water. They observe the water’s temperature to drop from 27.4°C to 15.3°C.

1. Is the dissolving of ammonium nitrate an endothermic or an exothermic process? 
   
   Check Answer
   Answer:  Endothermic
   
   The surroundings (water in the calorimeter) are cooling down so the surroundings are losing heat and the system is gaining heat. Heat enters the system for endothermic processes. 
   
    
   
    
2. Determine the quantity of heat exchanged between the system (reactants and products) and the surroundings (water in the calorimeter). 
   
   Check Answer
   Answer:  2.53 kJ from surroundings to system (that's what the - value on Q tells us)
   
   Use Q = m•C•∆T with 
   m = 50.0 g, C = 4.184 J/g/°C, and ∆T = 15.3°C - 27.4°C = -12.1°C
   
   Q = (50.0 g)•(4.184 J/g/°C)•(-12.1°C) = -2531.32 J
   Q = -2.53 kJ
    
   
    
3. Determine the number of moles of solid that were dissolved. 
   
   Check Answer
   Answer:  n = 0.100 mol
   
   Molar mass of NaOH is 39.997 g/mol
   The number of moles of NaOH is ...
   
   n = 4.00 g NaOH • (1 mol NaOH / 39.997 g NaOH) = 0.100007501 mol
   n = 0.100 mol (rounded)
   
    
   
    
4. Determine the heat of solution of NH₄NO₃ in kJ/mol. Be sure to include the proper + or - sign. 
   
   Check Answer
   Answer:  ∆H = +25.3 kJ/mol
   
   Q_system = +2.53132 kJ (+ since the heat entered the system)
   n = 0.100007501 mol
   
   ∆H = (+2.53132 kJ) / (0.100007501 mol) = 25.31130 ... kJ/mol
   ∆H = +25.3 kJ/mol