Lesson 1: Energy and Heat

Part d: Calorimetry

Part a: Energy
Part b: Heat and Temperature
Part c: Chemical Reactions and Energy
Part d: Calorimetry
Part e: Energy and Changes of State 

 

What is Calorimetry?

As we discussed on the previous page, reactions involve changes in the chemical potential energy of the system. Energy is either released by the system to the surroundings (exothermic) or absorbed by the system from the surroundings (endothermic). Chemists, and chemistry students, are often assigned the task of determining the amount of energy that is absorbed by or released by the system. To do so, an experimental technique known as calorimetry is used. Calorimetry relies on temperature change measurements to determine the amount of heat involved in chemical reactions and phase changes.
 
Students enrolled in a Chemistry course will likely do labs using a coffee cup calorimeter. A reaction or a phase change is performed in a water filled coffee cup. As usual, the chemicals (reactants and products) are considered the system. The surroundings are the rest of the universe. There is an exchange of heat between the system and the surroundings that results in a measurable temperature change of the water. The coffee cup provides insulation that limits the amount of interference that the rest of the universe has on the water. When equipped with a suitable lid, very little heat is exchanged between the water and the room, thus narrowing the surroundings from the rest of the universe to the water in the cup. This allows one to assume that the energy change of the system is equal and opposite to the energy change of the water in the coffee cup. This is consistent with the law of conservation of energy.

 

Energy Units

This is the first time in this Chemistry Tutorial that energy as a quantity has come up. As a quantity, energy is expressed in the metric unit known as the joule, abbreviate J. Because a joule is a relatively small amount of energy, we will often use the unit kilojoule (abbreviated kJ). From our understanding of metric prefixes, we know that …

1 kJ = 1000 J
 

 
 

Specific Heat Capacity

There was an unanswered question back in Lesson 1b. We discussed a hot piece of metal at 90°C placed in a container of chilled water at 10°C. Heat flowed from the metal to the water until the two objects reached thermal equilibrium. This occurred at 36°C. It did not occur at the midpoint temperature. An emphasis was placed on the fact that the quantity of heat lost by the metal was equal to the quantity of heat gained by the water. Yet the effects of those energy changes was not the same for the water as it was for the metal. Why?
 

 
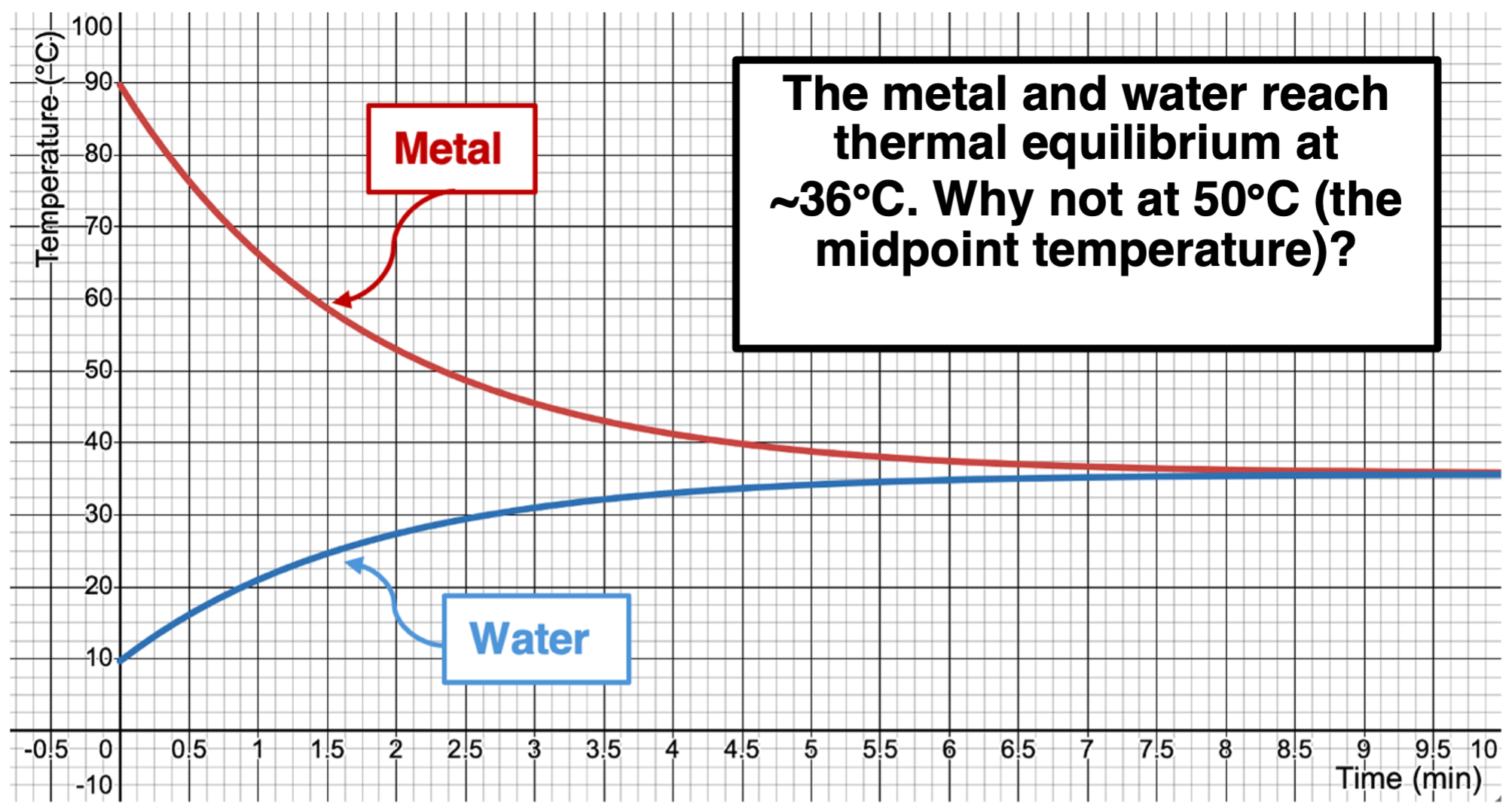
There are two variables that affect the temperature change of a sample when it absorbs (or releases) a given quantity of heat. The first is the material that the sample of matter is made of. The second is the mass of the sample. Water and metals are quite different in terms of their temperature change response to the absorption (or release) of heat. Water is generally VERY resistant to change its temperature when absorbing heat. Water has a lot of thermal inertia … resistance to temperature change when absorbing heat. Metals generally have a low thermal inertia. A relatively small loss or gain of energy results in a more dramatic temperature change.
 
The specific heat capacity provides a measure of this thermal inertia. We will define specific heat capacity as the amount of heat that is required to change the temperature of 1.00 gram of a substance by 1.00 °C. Different substances have different specific heat capacity values. The higher that the value is, the more heat that would be required to raise the temperature of that sample. Values for a variety of materials are shown in the table. Observe that water has the highest value of those listed.
 
In saying that the specific heat capacity of water is 4.184 J/g/°C, we mean that water must absorb 4.184 J to raise the temperature of a 1.00 gram sample by 1.00°C. The value for the J of heat can be scaled proportionally for samples of larger mass and for larger temperature changes. Here are several additional statements that can be made based on this 4.184 value:

• It takes 41.84 J of heat to raise the T of 10.0 g of H₂O by 1.00°C.
• It takes 41.84 J of heat to raise the T of 1.00 g of H₂O by 10.0°C.
• It takes 41.84 J of heat to raise the T of 5.00 g of H₂O by 2.0°C.
• It takes 418.4 J of heat to raise the T of 10.0 g of H₂O by 10.0°C.
• It takes 418.4 J of heat to raise the T of 100 g of H₂O by 1.00°C.
• It takes 418.4 J of heat to raise the T of 1.00 g of H₂O by 100°C.
• It takes 4184 J of heat to raise the T of 1000 g of H₂O by 1.00°C.
• Etc. Etc. Etc.

   
 

The Calorie Thing

We discussed the joule and kilojoule above. There are two other units that are commonly used; they are the calorie (abbreviated as cal) and the kilocalorie (abbreviated kcal). They have been defined based on the specific heat capacity of water. By definition, 1.00 calorie (with a lower-case c) is the amount of heat that would raise the temperature of 1.00 g of water by 1.00 °C. The specific heat capacity of water is 1.00 cal/g/°C. And so,
   
And as you would expect, 1 kilocalorie is equivalent to 1000 calories.
   

 

What About Nutritional Calories?

 
 
 
 

The Q Equation

How do we put all this together to determine the amount of heat gained or lost during a chemical reaction using a coffee cup calorimeter? This task is usually accomplished by using the Q equation:

Q = m•C•∆T

 In the equation,

• Q represents the quantity or amount of heat gained or lost by the sample
• m represents the mass of the sample
• C represents the specific heat capacity of the material (4.184 J/g/°C for H₂O)
• ∆T represents the temperature change of the sample

 
To see how the equation is used, let’s step through a couple of example problems.
 

Example 1

A 100.0-gram sample of water (C_water = 4.184 J/g/°C) absorbs heat and increases its temperature by 43.2°C. Calculate the quantity of heat (in kilojoules) that was absorbed by the water.
 

Solution:

Given:  m_water = 100.0 g, ∆T_water = 43.2°C, C_water = 4.184 J/g/°C
Determine: Q_water = ???
 
You know everything in the Q = m•C•∆T formula that is required to calculate the value of Q. Perform substitutions into the formula to solve for Q.
 
Q_water = m_water•C_water•∆T_water = (100.0 g)•(4.184 J/g/°C)•(43.2°C)
Q_water= 18074.88 J
Q_water = 18.1 kJ (rounded from 18.07488 kJ)
 
 

Example 2

A 200.0-gram sample of an unknown substance gains 836 J of energy. The sample increases its temperature by 12.4°C. Determine the specific heat capacity of the substance.
 

Solution:

Given:  m_substance = 200.0 g, ∆T_substance = 12.4°C, Q_substance = 836 J
Determine: C_substance = ???
 
The Q = m•C•∆T formula can be rearranged to solve for C. By dividing both sides of the equation by m and by ∆T, the following formula is derived:
 
C = Q/(m•∆T)
 
Known values can be substituted into the formula in order to solve for C.
 
C_substance = Q_substance/(m_substance•∆T_substance)
C_substance = (836 J)/( (200.0 g)•(12.4 °C) )
C_substance = 0.337 J/g/°C
 

  

Coffee Cup Calorimetry

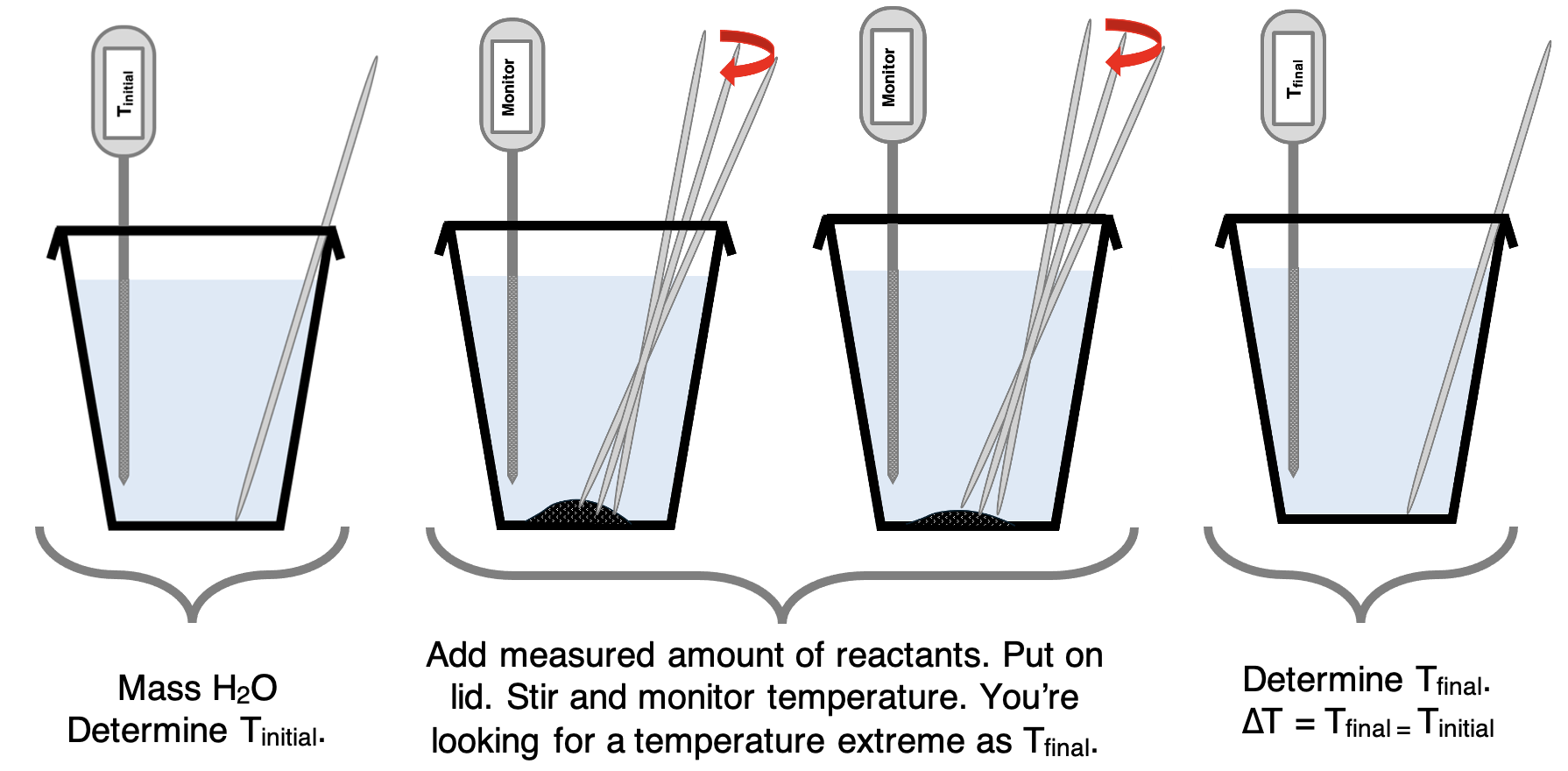
A mentioned earlier, the coffee cup calorimeter is the main experimental apparatus in the Chemistry lab during a Thermal Chemistry unit. It is used in experiments to determine the amount of heat released or absorbed by the reaction of a given amount of reactant. The coffee cup calorimeter is filled with water that absorbs the heat released in exothermic reactions and provides the heat that is required for endothermic reactions. The reaction takes place in the water and the water changes its temperature. The reactant chemicals are considered the system. The water is considered the surroundings.
 
The typical procedure involves preparing your coffee cup calorimeter by gathering the materials, adding a known mass of water, and measuring the initial temperature. Then immediately add the reactants to the water, put the lid on the cup, stir (with a stirring rod), and monitor the temperature. The temperature will either increase or decrease and will likely do it very quickly. Once all the reactants have completely reacted, the temperature will soon stop increasing (for exothermic reactions) or decreasing (for endothermic reactions). At that point, record the temperature extreme as the final temperature. The temperature change (∆T) is the difference between the final temperature and the initial temperature.

∆T = T_final - T_initial

A positive ∆T indicates an exothermic reaction since the temperature of the surroundings (water) increases. A negative ∆T indicates an endothermic reaction.
 

 
Let’s do a couple of examples to demonstrate how to use calculated data to determine the amount of heat released or absorbed by the system during a reaction.
 

 

 

Example 3

A student conducts an experiment to determine the amount of heat released for the following exothermic reaction:

Ca(s)  + 2 H₂O(l)  →  Ca(OH)₂(aq)  +  H₂(g)  +  Energy

 A student prepares the calorimeter with 50.0 mL of water chilled to an initial temperature of 12.5°C. (Density of H₂O is 1.00 g/mL.) After adding 2.02 g of Ca, the temperature quickly rises to a final temperature of 42.8°C. Perform calculations to determine …
a. The quantity or amount of heat released by the system to the calorimeter in kilojoules.
b. The quantity of heat released per gram of calcium.
c. The quantity of heat released per mole of calcium.
 
 

Solution:

Part a:
Use the Q = m•C•∆T equation to calculate Q - the quantity of heat absorbed by the surroundings. This is equal to the quantity of heat released by the system.
 
Given:  m_water = 50.0 g, T_initial = 12.5°C, T_final = 42.8°C, C_water = 4.184 J/g/°C
 
Begin by calculating ∆T as ∆T = T_final - T_initial = 42.8°C - 12.5°C = 30.3°C
 
Now you know everything in the Q = m•C•∆T equation. Calculate Q.
 
Q = m•C•∆T = (50.0 g)•(4.184 J/g/°C)•(30.3°C) = 6338.76 J
Q = 6.34 kJ (rounded from 6.33876 kJ)
 
 
Part b
Having done Part a, we know that 6.33876 kJ of heat are released when 2.02 g of Ca react. We can now determine the heat released in kJ per gram. “Per gram”, written as “/gram” or “/g” indicates that the quantity of heat must be divided by the mass in grams.
 
(6.33876 kJ) / (2.02 g) = 3.14 kJ/g  (rounded from 3.138 kJ/g)
 
 
Part c
Now that we have the heat released in kJ per gram of Ca, we can use the molar mass of Ca to determine the value in kJ per mole. One means of doing this is by use of a molar mass conversion factor. Using the factor label method helps answer the question as to whether you should multiply by molar mass or divide by molar mass. The question actually becomes, how do I cancel grams and get moles in the denominator.
 
The set-up is shown here:
 

 
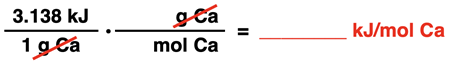
The molar mass of Ca is 40.078 g/mol (from the Periodic Table). The 40.078 is inserted in the numerator next to the unit g and a 1 is inserted next to mol in the denominator.
 

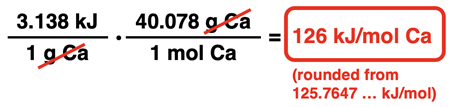
This final value is sometimes referred to as the heat of reaction. It is the amount of heat released per mole of calcium that reacts.

 

 

Example 4

The dissolving of ammonium nitrate in water is an endothermic process.

Energy  +  NH₄NO₃(s)  →  NH₄⁺(aq)  +  NO₃^-(aq)

A student conducts an experiment to determine the amount of heat absorbed by the system when undergoing the reaction. A student prepares the calorimeter with 50.0 mL of warm water an initial temperature of 40.2°C. (Density of H₂O is 1.00 g/mL.) After adding 20.18 g of NH₄NO₃, the temperature quickly drops to a final value of 11.9°C. As shown in the data, the calorimeter (water) cooled down, indicating that the reaction is endothermic. The calorimeter (surroundings) transferred energy to the system (NH₄NO₃). Perform calculations to determine …
a. The quantity or amount of heat transferred from the calorimeter in kilojoules.
b. The quantity of heat absorbed by the system per gram of NH₄NO₃.
c. The quantity of heat released by the system per mole of NH₄NO₃.
 
 

Solution:

Part a:
Use the Q = m•C•∆T equation to calculate Q - the quantity of heat transferred by the surroundings to the system. This is equal to the quantity of heat absorbed by the system.
 
Given:  m_water = 50.0 g, T_initial = 40.2°C, T_final = 11.9°C, C_water = 4.184 J/g/°C
 
Begin by calculating ∆T as ∆T = T_final - T_initial = 11.9°C - 40.2°C = -28.3°C
(The - indicates a temperature decrease in the surroundings.)
 
Now you know everything in the Q = m•C•∆T equation. Calculate Q.
 
Q = m•C•∆T = (50.0 g)•(4.184 J/g/°C)•(-28.3°C) = -5920.36 J
Q = -5.92 kJ (rounded from -5.92036 kJ)
(The - value on Q indicates that the water lost heat to the system. The reaction is endothermic.)
 
 
Part b
Having done Part a, we know that 5.92036 kJ of heat are absorbed by the system when 20.18 g of NH₄NO₃ dissolve. We can now determine the heat absorbed in kJ per gram. “Per gram”, written as “/gram” or “/g” indicates that the quantity of heat must be divided by the mass in grams.
 
NOTE: We will drop the - sign in the calculations that follow as it has nothing to do with the quantity of heat; it only indicates the direction that the heat is being transferred … to the system from the surroundings.)
 
(5.92036 kJ) / (20.18 g) = 0.293 kJ/g  (rounded from 0.2933776 … kJ/g)
 
 
Part c
Now that we have the heat absorbed in kJ per gram of NH₄NO₃, we can use the molar mass of NH₄NO₃ to determine the value in kJ per mole. We will once again use a molar mass conversion factor. The set-up is shown here:
 

 
The molar mass of NH₄NO₃ is 80.043 g/mol (from the Periodic Table). The 80.043 is inserted in the numerator next to the unit g and a 1 is inserted next to mol in the denominator.
 

 
This final value is sometimes referred to as the heat of reaction or even the heat of solution. It is the amount of heat absorbed per mole of NH₄NO₃ that dissolves.
 
 
 
 

Before You Leave

• Download our Study Card on Calorimetry. Save it to a safe location and use it as a review tool. (Coming Soon.)
• Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Thermal Chemistry page. Check out the following problem sets:
  • Problem Set TC1: Specific Heat Capacity
  • Problem Set TC2: Calorimetry 1
  • Problem Set TC3: Calorimetry 2
• Need more practice? Try our Measuring the Quantity of Heat Concept Builder.
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Coffee cup calorimetry is based on the idea that the energy change of the system of chemicals is equal to the energy change of the water. Are there any conditions under which this would not be true? Explain your answer.

 
 
 
2. Substance A has twice the specific heat capacity as Substance B. This means that _______.

1. Substance A can absorb twice the heat as Substance B.
2. Substance A will expereince twice the temperature change as Substance B.
3. When two same-mass samples absorb the same amount of heat, Substance A will have twice the temperature change.
4. In order for two same-mass samples to have the same temperature change, Substance A must absorb twice as much heat.

 

 
 
 
3. A substance has a specific heat capacity of 2.0 J/g/°C. Complete the following sentences.

1. A 100.0-g sample must absorb ______ J of heat to change its temperature by 1°C. 
   
   See Answer
   Answer: 200 J
   
   Q = m•C•∆T = (100.0 g)•(2.0 J/g/°C)•(1°C) = 200 J
   
    
   
    
2. A 100.0-g sample must absorb ______ J of heat to change its temperature by 10°C. 
   
   See Answer
   Answer: 2000 J
   
   Q = m•C•∆T = (100.0 g)•(2.0 J/g/°C)•(10°C) = 2000 J
   
    
   
    
3. A 50.0-g sample must absorb ______ J of heat to change its temperature by 1°C. 
   
   See Answer
   Answer: 100 J
   
   Q = m•C•∆T = (50.0 g)•(2.0 J/g/°C)•(1°C) = 100 J
   
    
   
    
4. A 50.0-g sample must absorb ______ J of heat to change its temperature by 10°C. 
   
   See Answer
   Answer: 1000 J
   
   Q = m•C•∆T = (50.0 g)•(2.0 J/g/°C)•(10°C) = 1000 J
   
    
   
    
5. A 200.0-g sample must absorb ______ J of heat to change its temperature by 5°C. 
   
   See Answer
   Answer: 2000 J
   
   Q = m•C•∆T = (200.0 g)•(2.0 J/g/°C)•(5°C) = 2000 J
   
    
   
    

 
 
4. Consider a 10.0-gram sample of a particular metal that has a specific heat capacity of 0.60 J/g/°C. Complete the following sentences.

1. When the metal sample gains 24.0 J of heat, its temperature will increase by _____ °C. 
   
   See Answer
   Answer: 4.00°C
   
   ∆T = Q/(m•C) = 24.0 J /( (0.600 J/g/°C)•(10.0 g) ) = 4.00 °C
   
   
    
   
    
2. When the metal sample gains 48.0 J of heat, its temperature will increase by _____ °C. 
   
   See Answer
   Answer: 8.00°C
   
   ∆T = Q/(m•C) = 48.0 J /( (0.600 J/g/°C)•(10.0 g) ) = 8.00 °C
   
    
   
    
3. When the metal sample gains 120.0 J of heat, its temperature will increase by _____ °C. 
   
   See Answer
   Answer: 20.0°C
   
   ∆T = Q/(m•C) = 120.0 J /( (0.600 J/g/°C)•(10.0 g) ) = 20.0 °C
   
    
   
    
4. When the metal sample gains 240.0 J of heat, its temperature will increase by _____ °C. 
   
   See Answer
   Answer: 40.0°C
   
   ∆T = Q/(m•C) = 240.0 J /( (0.600 J/g/°C)•(10.0 g) ) = 40.0 °C
   
    
   
    
5. When the metal sample gains 480.0 J of heat, its temperature will increase by _____ °C. 
   
   See Answer
   Answer: 80.0°C
   
   ∆T = Q/(m•C) = 480.0 J /( (0.600 J/g/°C)•(10.0 g) ) = 80.0 °C
   
    
   
    

 
 
5. Ray Ahn and Polly Ester are doing the Specific Heat of a Metal lab. Their 63.55-gram sample of unknown metal is placed in a beaker of water. They determine that a metal cools from 95.4°C to 31.5°C. In the process, it loses 1563 J of heat to the water. What is its specific heat capacity?

 
 
 
6. A 167.9 g sample of water at 80.4°C loses 47840 J of heat.
a. Calculate the temperature change of the water. (Enter a – answer if appropriate.) 


b. Calculate the final temperature of the water. (Enter a – answer if appropriate.) 



 
 
7. In order to determine the Calorie content of cheese pizza, a nutritional chemist burns a 2.44-gram sample of the pizza in a bomb calorimeter containing 487.7 grams of water. The pizza sample is burned and the calorimeter increases its temperature by 14.4°C.
a. What quantity of heat was absorbed by the water (in kJ)?
b. Convert this quantity to nutritional Calories. Given: 1.00 J = 0.000239 Calories (nutritional).
c. What is the Calorie content of the pizza in Calories/gram?