Lesson 1: Energy and Heat

Part e: Energy and Changes of State

Part a: Energy
Part b: Heat and Temperature
Part c: Chemical Reactions and Energy
Part d: Calorimetry
Part e: Energy and Changes of State

 

Heating Curves Revisited

The topic of changes of state was discussed in Lesson 2a of Chapter 11 of this Chemistry Tutorial. While we often discuss six changes of state, the focus on this page will be upon melting (a.k.a., fusion) and vaporization (which includes boiling).
 
In Chapter 11, we introduced the idea of a heating curve using a thought experiment. If we were to heat a sample of ice at -20°C in a closed container to a temperature of 120°C, we can imagine five different changes that would occur:

1. The ice first would undergo a temperature change until it reaches its melting temperature of 0°C.
2. At the melting point, the ice would undergo a state change from a solid to a liquid. The ice would melt while the temperature remained constant at 0°C.
3. Once all the ice was melted, the liquid water would undergo a temperature change until it reaches its boiling point of 100°C.
4. At the boiling point, the liquid would undergo a state change from the liquid to the vapor state. The water would boil while the temperature remained constant at 100°C.
5. Once all the liquid water was boiled, the water vapor would undergo a temperature change to 120°C. At this point, we turn off the heat and our (thought) experiment ends.

 
If this 5-stage process was represented on a graph of temperature vs. heat added, it would look like the graph below. This graph is referred to as a heating curve.
   
Note that there are three diagonal lines on the graph that are associated with temperature changes. And there are two horizontal lines on the graph that are associated with state changes. Energy (in the form of heat) is required for all five stages. The amounts can be calculated. For the diagonal lines (temperature changes), the amount of required heat can be calculated using the Q = m•C•∆T equation. For the horizontal lines (state changes), the amount of required heat can be calculated using heat of fusion and heat of vaporization values.
   
 

Heat of Fusion

Fusion is the process of changing the state of a substance from a solid to a liquid. Fusion is more commonly referred to as melting. Because fusion requires that the intermolecular forces holding particles in the solid state be overcome, the process requires energy. That is, fusion is an endothermic process.
 
The amount of energy required to change a solid to a liquid at its melting point is known as the heat of fusion.  The strength of the intermolecular forces between solid particles varies from substance to substance. Thus, different substances have different heat of fusion values. Values for a sampling of materials are shown in the table at the right. Values for heat of fusion are typically expressed in kilojoules per mole (kJ/mol, as shown) or in joules/gram (J/g). When expressed in units of kJ/mol, the value is referred to as the molar heat of fusion.
 
Using the factor label method, a heat of fusion value can be used to determine the amount of energy required to melt a given amount of a substance. For instance, let’s suppose that we wish to determine the amount of energy required to melt a 100.0-gram sample of ice. The mass of the sample, the molar mass of ice (H₂O), and the molar heat of fusion can be used to determine the amount of energy required to melt the 100.0-g ice sample.
   
Observe how the conversion factors - molar mass and molar heat of fusion - are arranged to cancel units  (grams and moles) with kilojoules remaining as the uncancelled unit.
 
 
 

Heat of Vaporization

Vaporization is the process of changing the state of a substance from a liquid to a gas (or vapor). When done at the boiling point, the process is referred to as boiling. An ideal gas experiences no intermolecular forces. A liquid does experience intermolecular forces that prevent particles from filling the entire container. Boiling is an endothermic process that supplies a liquid sample with enough energy to allow partciles to overcome the forces that hold them together in the liquid state.
 
The amount of energy required to change a liquid to a gas at its boiling point is known as the heat of vaporization.  Different substances have different heat of vaporization values. Values for a sampling of materials are shown in the table at the right. Values for heat of vaporization are typically expressed in kilojoules per mole (kJ/mol as shown) or in joules/gram (J/g). When expressed in units of kJ/mol, the value is referred to as the molar heat of vaporization.
 
Similar to the calculation shown above, heat of vaporization values can be used as conversion factors to determine the amount of energy required to boil a given amount of substance. Suppose you wished to determine the amount of energy required to boil a 100.0-gram sample of liquid water. The mass, molar mass, and molar heat of vaporization can be combined to determine the amount of energy as shown below.
   
 
 

Analyzing a Heating Curve

Let’s put a small twist on our original thought experiment - heat a sample of ice at -20.0°C to a temperature of 120.0°C in a closed container. Let’s think through how we would determine the quantity of heat that would be required for such a change. We will assume that we start with a 100.0-gram sample of ice.  

 
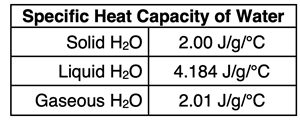
As we discussed earlier, this is a five-stage process. Three of the five stages involve a temperature change. The quantity of heat (Q) that is required for such temperature changes can be calculated using the equation Q = m•C•∆T where m is the mass of the sample, C is the specific heat capacity of the substance, and ∆T is the temperature change. The value of C is different for the solid, liquid, and gaseous state. Three calculations must be made - one for each of the stages involving a temperature change.
 
Two of the five stages involve a state change occurring at a constant temperature. The fusion of the ice occurs at 0.0°C. The vaporization of the liquid water occurs at 100.0°C. The quantity of heat (Q) that is required for such state changes can be calculated using the equations
   
where n is the number of moles of water and ∆H_fusion and ∆H_vaporization are the molar heat of fusion and the molar heat of vaporization values. For water, those values are 6.02 kJ/mol and 40.7 kJ/mol respectively. The value of n can be calculated from the mass in grams using the molar mass value of water.
 
The heating curve graph below summarizes the mathematical relationships discussed above.
   
Not every heating curve analysis involves a 5-stage calculation. For instance, consider the following two problems:

• Determine how much heat is required to change 100.0-g of water at 50.0°C to a gas at 120.0 °C.
• Determine how much heat is required to change 100.0-g of ice at 0.0°C to a gas at 100.0 °C.

 
Both of these problems would involve a 3-stage analysis. An understanding of heating curves makes the analysis considerably easier. Find your starting point and your final destination on the graph. Then determine how to proceed. This type of analysis is demonstrated below for the two stated problems. The complete mathematics is shown in Example 2 and Example 3.
     
 
The following examples are based on the discussion above. We recommend that you attempt the problem on your own and then tap the button to check your answer.
 
 

Example 1

Determine the total quantity of energy required to heat a 100.0-g sample of ice at -20.0°C to a temperature of 120.0°C.
 


 
 

Example 2

Determine how much heat is required to change 100.0-g of water at 50.0°C to a gas at 120.0 °C.
 


 
 
 

Example 3

Determine how much heat is required to change 100.0-g of ice at 0.0°C to a gas at 100.0 °C.
  



 
 
Comfort with solving chemistry problems always requires more than simply viewing textbook solutions. It is an endothermic process; it requires energy on the part of the student to gain comfort. Before continuing to Lesson 2, make sure you’re comfortable with the process. Use the suggestions below to grow your confidence in solving problems involving state changes.
 
 
 

Before You Leave

• Download our Study Card on Energy and State Changes. Save it to a safe location and use it as a review tool. (Coming soon.)
• Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Thermal Chemistry page. Check out the following problem set - Problem Set TC6: Heating Curves and Phase Changes.
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. What does a horizontal line on a heating curve represent?

 
 
 
2. What does a diagonal line on a heating curve represent?

​
 
 
 
3. When analyzing a heating curve to determine the quantity of heat added to a substance, when is the Q = m•C•∆T used?

​
 
 
 
4. The heat of fusion of candle wax is approximately 14.8 kJ/mol. Assuming wax is C₂₅H₅₂, determine …

1. … the molar mass of candle wax.
2. … the number of moles of C₂₅H₅₂ in 5.00 grams of C₂₅H₅₂.
3. … the quantity of heat required to melt 5.00 grams of C₂₅H₅₂.

​
 
 
 
5. The heat of vaporizaton of butane (C₄H₁₀) is 21.0 kJ/mol. Determine …

1. … the molar mass of butane.
2. … the number of moles of C₄H₁₀ in 1.00 gram of C₄H₁₀.
3. … the quantity of heat required to vaporize 1.00 gram of C₄H₁₀.

 
​
 
 
 
6. Liquid bromine (Br₂) has a heat of vaporization of 30.0 kJ/mol. What quantity of energy (in kilojoules) is required to vaporize 15.98 g of liquid bromine?

​
 
 
7. Determine the amount of heat required to increase the temperature of a 3.82-gram sample of solid para-dichlorobenzene from 24.0°C to its liquid state at 75.0°C. Para-dichlorobenzene has a melting point of 54.0°C, a heat of fusion of 124 J/g and specific heat capacities of 1.01 J/g/°C (solid state) and 1.19 J/g/°C (liquid state).

​
 
 
 
8. A 31.0-gram sample of frozen water at -12.7°C is warmed to its melting point and then melted. It is then warmed to a temperature of 22.2°C. Given:
Specific heat capacity of ice is 2.00 J/g/°C
Specific heat capacity of liquid water is 4.184 J/g/°C
Heat of fusion of water is 6.01 kJ/mol.
Determine …

1. … the quantity of energy (in kilojoules) required to warm the ice from -12.7°C to its melting point (0.0°C).
2. … the quantity of energy (in kilojoules) required to melt the ice.
3. … the quantity of energy (in kilojoules) required to warm the liquid water from 0.0°C to 22.2°C.
4. … the total quantity of energy (in kilojoules) required to change 31.0 g of solid water at -12.7°C to the liquid water at 22.2°C.

 

​