Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 Refraction is the bending of the path of a light wave as it passes from one material into another material. The refraction occurs at the boundary and is caused by a change in the speed of the light wave upon crossing the boundary. The tendency of a ray of light to bend one direction or another is dependent upon whether the light wave speeds up or slows down upon crossing the boundary. The speed of a light wave is dependent upon the optical density of the material through which it moves. For this reason, the direction that the path of a light wave bends depends on whether the light wave is traveling from a more dense (slow) medium to a less dense (fast) medium or from a less dense medium to a more dense medium. In this part of Lesson 1, we will investigate this topic of the direction of bending of a light wave.
Refraction is the bending of the path of a light wave as it passes from one material into another material. The refraction occurs at the boundary and is caused by a change in the speed of the light wave upon crossing the boundary. The tendency of a ray of light to bend one direction or another is dependent upon whether the light wave speeds up or slows down upon crossing the boundary. The speed of a light wave is dependent upon the optical density of the material through which it moves. For this reason, the direction that the path of a light wave bends depends on whether the light wave is traveling from a more dense (slow) medium to a less dense (fast) medium or from a less dense medium to a more dense medium. In this part of Lesson 1, we will investigate this topic of the direction of bending of a light wave.
Predicting the Direction of Bending
Recall the Marching Soldiers analogy discussed earlier in this lesson. The analogy served as a model for understanding the boundary behavior of light waves. As discussed, the analogy is often illustrated in a Physics classroom by a student demonstration. In the demonstration, a line of students (representing a light wave) marches towards a masking tape (representing the boundary) and slows down upon crossing the boundary (representative of entering a new medium). The direction of the line of students changes upon crossing the boundary. The diagram below depicts this change in direction for a line of students who slow down upon crossing the boundary.
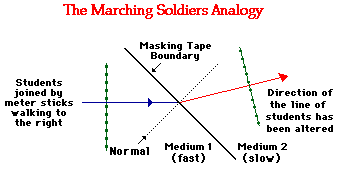
On the diagram, the direction of the students is represented by two arrows known as rays. The direction of the students as they approach the boundary is represented by an incident ray (drawn in blue). And the direction of the students after they cross the boundary is represented by a refracted ray (drawn in red). Since the students change direction (i.e., refract), the incident ray and the refracted ray do not point in the same direction. Also, note that a perpendicular line is drawn to the boundary at the point where the incident ray strikes the boundary (i.e., masking tape). A line drawn perpendicular to the boundary at the point of incidence is known as a normal line. Observe that the refracted ray lies closer to the normal line than the incident ray does. In such an instance as this, we would say that the path of the students has bent towards the normal. We can extend this analogy to light and conclude that:
|
Light Traveling from a Fast to a Slow Medium
If a ray of light passes across the boundary from a material in which it travels fast into a material in which travels slower, then the light ray will bend towards the normal line.
|
The above principle applies to light passing from a material in which it travels fast across a boundary and into a material in which it travels slowly. But what if light wave does the opposite? What if a light wave passes from a material in which it travels slowly across a boundary and into a material in which it travels fast? The answer to this question can be answered if we reconsider the Marching Soldier analogy. Now suppose that the each individual student in the train of students speeds up once they cross the masking tape. The first student to reach the boundary will speed up and pull ahead of the other students. When the second student reaches the boundary, he/she will also speed up and pull ahead of the other students who have not yet reached the boundary. This continues for each consecutive student, causing the line of students to now be traveling in a direction further from the normal. This is depicted in the diagram below.
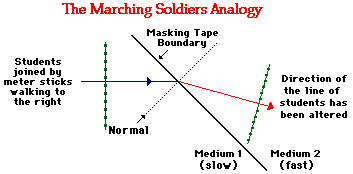
From this analogy and the diagram above, we see that the refracted ray (in red) is further away from the normal then the incident ray (in blue). In such an instance as this, we would say that the path of the students has bent away from the normal. We can once more extend this analogy to light and conclude that:
|
Light Traveling from a Slow to a Fast Medium
If a ray of light passes across the boundary from a material in which it travels slowly into a material in which travels faster, then the light ray will bend away from the normal line.
|
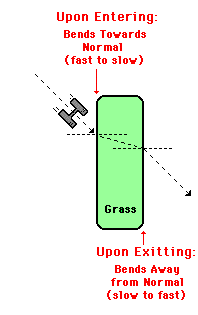
The Tractor Analogy
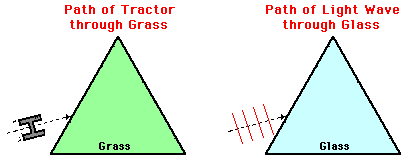
Now lets consider another analogy to assist in our understanding of these two important principles. Suppose that a tractor is moving across an asphalt surface towards a rectangular plot of grass (as shown in the diagram at the right). Upon entering the grass, the tractors' wheels will sink into the surface and slow down. Upon exiting the plot of grass on the opposite side, the tractor wheels will speed up and achieve their original speed. In effect, this analogy would be representative of a light wave crossing two boundaries. At the first boundary (the asphalt to grass boundary), the light wave (or the tractor) would be slowing down; and at the second boundary (the grass to asphalt boundary), the light wave (or the tractor) would be speeding up. We can apply our two important principles listed above and predict the direction of bending and the path of the tractor as it travels through the rectangular plot of grass. As indicated on the diagram, upon entering the grass, the wheels slow down and the path of the tractor bends towards the normal (perpendicular line drawn to the surface). Upon exiting the plot of grass, the wheels speed up and the path of the tractor bends away from the normal. The path of the tractor is closer to the normal in the slower medium and farther away from the normal in the faster medium.
This analogy can be extended to the path of a light wave as it passes from air into and out of a rectangular block of glass. Since air is less optically dense than glass, the light wave will slow down upon entering the glass and speed up when exiting the glass. In other words, the light wave will 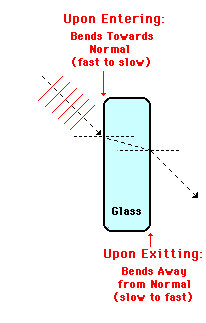 be undergoing the same change in speed as the tractor in the above diagram. For this reason, the direction of bending for the light wave upon entering and exiting the glass will be the same as in the diagram above. The light ray refracts towards the normal upon entering the glass (crossing from a fast to a slow medium) and refracts away from the normal upon exiting the glass (crossing from a slow to a fast medium). This is shown in the diagram at the right.
be undergoing the same change in speed as the tractor in the above diagram. For this reason, the direction of bending for the light wave upon entering and exiting the glass will be the same as in the diagram above. The light ray refracts towards the normal upon entering the glass (crossing from a fast to a slow medium) and refracts away from the normal upon exiting the glass (crossing from a slow to a fast medium). This is shown in the diagram at the right.
There is an important point to be noted in these diagrams of the rectangular plot of grass and rectangular block of glass. Notice that the direction of the original incident ray is the same as the direction of the final refracted ray. Put another way, the direction at which the light is traveling when entering the rectangular block of glass is the same as the direction that the light travels after exiting the rectangular block of glass. There is no ultimate change in the direction that the light is traveling. This small detail will only be the case under two conditions:
- the two sides of the glass through which the light enters and exits are parallel to each other
- the medium surrounding the glass on the side through which the light enters and exits are the same
These two conditions are met in the case of a rectangular block of glass surrounded by air.
The diagrams below provide a contrast to the rectangular plot of grass and the rectangular block of glass. Both diagrams involve the refraction of a tractor or a light wave as it passes into and out of a triangular plot of grass and a triangular block of glass.
 Copy this diagram onto a sheet of paper and apply your understanding of refraction principles to predict the path of the tractor and the light wave as it travels through the triangle-shaped obstacle. Draw the path on your separate sheet of paper and then click on the button below to check your answer
Copy this diagram onto a sheet of paper and apply your understanding of refraction principles to predict the path of the tractor and the light wave as it travels through the triangle-shaped obstacle. Draw the path on your separate sheet of paper and then click on the button below to check your answer
Least Time Principle
Another means of approaching the subject of the direction that light bends when crossing a boundary between two media is through the Least Time Principle. This Least Time Principle is sometimes stated as follows:
|
Least Time Principle
Of all the possible paths that light might take to get from one point to another, it always takes the path that requires the least amount of time.
|
A useful analogy to understanding the principle involves a lifeguard who has become aware of a drowning swimmer in the water. In order to save the drowning swimmer, the lifeguard must run through the sand, cross the boundary between the sand and the water, and then swim through the water to the drowning swimmer. Of course, the guard must reach the swimmer in as little time as possible. Since the guard can run faster on sand than she can swim in water, it would make sense that the guard covers more distance in the sand than she does in the water. In other words, she will not run directly at the drowning swimmer. The optimal entry point into the water is the point that would allow the lifeguard to reach the drowning swimmer in the least amount of time. Obviously, this point would be at a location closer to the swimmer than to the guard. The diagram below depicts such an entry point.
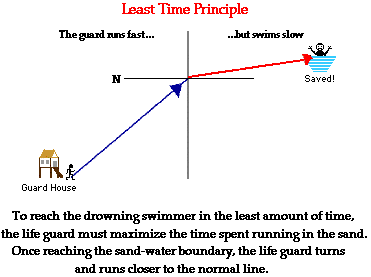
Observe in the diagram, that minimizing the time to reach the swimmer means that the lifeguard will approach the boundary at a steep angle to the normal and then will bend towards the normal upon crossing the boundary. This analogy demonstrates that the Least Time Principle would predict the following direction of bending:
A ray of light will bend towards the normal when crossing the boundary from a medium in which it travels fast into a medium in which it travels slowly.
This is the very generalization that was made earlier on this page.
Some Useful Mnemonics
Using the above principles and logic to explain and predict the direction that light refracts when crossing a boundary will be a major objective of this unit. Rather than merely restating the principle, you will be asked to apply it to a variety of situations (such as those in the Check Your Understanding section below). Part of accomplishing this task will involve remembering the principles. For this reason, the following useful mnemonics are offered.
|
FST = Fast to Slow, Towards Normal
If a ray of light passes across the boundary from a material in which it travels fast into a material in which travels slower, then the light ray will bend towards the normal line.
|
|
SFA = Slow to Fast, Away From Normal
If a ray of light passes across the boundary from a material in which it travels slow into a material in which travels faster, then the light ray will bend away from the normal line.
|
A mnemonic is a tool used to help one remember and difficult-to-remember idea. Of course, there is always the risk that the mnemonic will be forgotten. And since FST and SFA might not be the most easily remembered mnemonics, perhaps the following oddity will help. You can remember FST (fast to slow; towards) by simply thinking about those Freaky Science Teachers that you have had through the years. And you can remember SFA by thinking about the disgusting habit of your friend Sara (or Susan or Sammy or Samir or Somebody ...) - Sarah Farts Alot.
Flickr Physics Photo
Laser light shown passing through a rectangular block of lucite. It bends towards the normal as it enters the lucite. As it exits the lucite into air, it bends away from the normal.

We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Refraction Interactive or our
Least Time Principle Interactive. You can find these in the Physics Interactives section of our website. These Interactives provide the learner an interactive enivronment for exploring the refraction and/or reflection of light at a boundary between two materials.
Check Your Understanding
Test your ability to apply these principles by answering the following questions.
1. When light passes from a more optically dense medium into a less optically dense medium, it will bend _______ (towards, away from) the normal.
2. When light passes from a less optically dense medium into a more optically dense medium, it will bend _______ (towards, away from) the normal.
3. When light passes from a medium with a high index of refraction value into a medium with a low index of refraction value, it will bend _______ (towards, away from) the normal.
4. When light passes from a medium with a low index of refraction value into a medium with a high index of refraction value, it will bend _______ (towards, away from) the normal.
5. In each diagram, draw the "missing" ray (either incident or refracted) in order to appropriately show that the direction of bending is towards or away from the normal.
6. Arthur Podd's method of fishing involves spearing the fish while standing on the shore. The actual location of a fish is shown in the diagram below. Because of the refraction of light, the observed location of the fish is different than its actual location. Indicate on the diagram the approximate location where Arthur observes the fish to be. Must Arthur aim above or below where the fish appears to be in order to strike the fish?

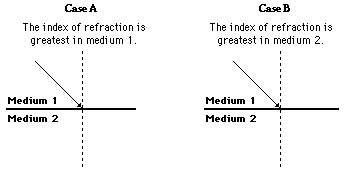
7. For the following two cases, state whether the ray of light will bend towards or away from the normal upon crossing the boundary.