Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 1: Kinetics of Reactions
Part d: Rate Equations
Part a:
Reaction Rates
Part b:
Factors Affecting Reaction Rates
Part c:
The Collision Model of Reactions
Part d: Rate Equations
Part e:
Reaction Mechanisms
What is a Rate Equation?
As we discussed in Lesson 1b, the rate of a reaction is dependent upon the concentration of the reactants. A rate equation, sometimes referred to as a rate law, provides a quantitative description of the dependence of the reaction rate upon concentration. Such equations are often called differential rate equations. Later in Lesson 1d, we will briefly discuss integrated rate equations which describe how the concentration of a reactant changes with time.
Suppose we have a reaction that has the form of
A + B → Products
where A and B are generic reactants. An experimental study must be done to identify the specifics of the rate equation. We would expect the specifics to show that the rate is dependent upon the concentration of one or both of the reactants. Possible rate equations might include any one of the following:
Rate = k•[A]1
Rate = k•[B]1
Rate = k•[A]2
Rate = k•[B]2
Rate = k•[A]1•[B]1
Rate = k•[A]2•[B]1
Rate = k•[A]1•[B]2
where
k is a numerical value known as the rate constant,
[A] refers to the
molar concentration of reactant A, and
[B] refers to the
molar concentration of reactant B. As you can see, a rate equation has the generic form of
Rate = k•[A]x•[B]y
where x and y are exponents or powers (usually whole numbers like 0, 1, or 2). The rate constant and the exponents are determined by experiment.
 The Method of Initial Rates
The Method of Initial Rates
There are numerous experimental methods for determining the rate equation for a reaction. We will discuss one method known as the method of initial rates. The method of initial rates involves conducting several trials with varying initial concentrations of reactants in order to determine the initial rate of the reaction. From trial to trial, the concentration of one of the reactants is modified, usually by halving, doubling, or even tripling the value. The initial rate is determined. Since reactant concentrations will change as the reaction proceeds, it is important to measure an initial rate that is consistent with the concentrations that were initially used. By carefully controlling the molar concentrations of reactants in each trial and measuring an initial rate, the data can be analyzed to determine a rate equation.
The method of initial rates yields a data set with reactant concentrations and the corresponding rate values. A sample data set is shown below.
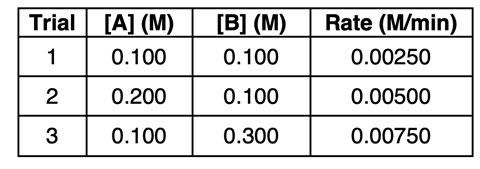
It is important to first make observations of how a doubling, tripling, quadrupling, or halving of a concentration affects the rate. Comparing trials 1 and 2, you observe that the concentration of reactant A was doubled. The effect of this doubling of [A] is that the rate of reaction was doubled. And in comparing trials 1 and 3, you observe that the concentration of reactant B was tripled. The effect of this tripling of [B] is that the rate of reaction was tripled. These observations allow you to determine the exponents x and y in the rate equation that has the form of Rate = k•[A]x•[B]y. Here are some general rules that you can apply to determine the exponents x and y:
- If doubling [A] causes a doubling of the rate, then the exponent on [A] is 1.
- If tripling [A] causes a tripling of the rate, then the exponent on [A] is 1.
- If doubling [A] causes a quadrupling of the rate, then the exponent on [A] is 2.
- If tripling [A] causes the rate to be nine times larger, then the exponent on [A] is 2.
- If doubling [A] has no effect upon the rate, then the exponent on [A] is 0.
The rules have been expressed in terms of reactant A. They can be equally applied to reactant B. They can also be applied in a similar manner to situations in which a concentration is quadrupled or halved. For the data set shown above, the rate equation would have the form of
Rate = k•[A]1•[B]1
And of course, since not displaying an exponent means it is assumed to be 1, the exponents could be removed for both reactants.
We show several examples below using generic reactants A and B. We have included additional practice in our
Check Your Understanding section that are based on actual reactions.
Determining the Rate Constant
A rate equation is not complete until the value of the rate constant
k is determined. Once you know the values of the exponent on [A] and [B], it is easy to use the data to determine the rate constant. Isolate any one of the trials and substitute the known concentration and rate values into the rate equation. Then solve for the value of k.

Let’s perform this task for Trial 1 in the data set above. We know that …
Rate = k•[A]1•[B]1
and we know the values of Rate, [A], and [B]. Substituting, we get …
0.00250 M/min = k•(0.100 M)1•(0.100 M)1
Rearranging, we get …
k = (0.00250 M/min) / [(0.100 M)1•(0.100 M)1]
k = 0.250 /M/min
We can now write the complete rate equation for our sample data set. It is …
Rate = (0.250 /M/min)•[A]1•[B]1
The value of the rate constant is unique to every reaction for a particular temperature. Thus, it does not matter which trial we pick to perform our rate constant calculation. If we had picked Trial 3 instead of Trial 1, our calculation would look different but the resulting k value would be the same.

For Trial 3, we would set up our rate equation as follows:
0.00750 M/min = k•(0.100 M)1•(0.300 M)1
Rearranging, we get …
k = (0.00750 M/min) / [(0.100 M)1•(0.300 M)1]
k = 0.250 /M/min
It is the same rate constant value.
The units on the rate constant can be quite troublesome for many students. Complicating the issue is that they won’t be the same unit for every reaction. The actual units are best determined by including units when setting up of the calculations. That is, put units on the rate (always M divided by a time unit) and put units on the concentration (always M). Be sure to consider the exponent - 0, 1, or 2 - on the concentrations. Then determine the result of the rate unit divided by the concentration units. Here’s some examples.
Example 1
The method of initial rates is used to acquire the following data set. Determine the rate equation (including the value of k).
Solution
An inspection of trials 1 and 2 shows that a doubling of [A] causes a doubling of the reaction rate. Thus, the exponent on [A] in the rate equation is 1. An inspection of trials 1 and 3 shows that a doubling of [B] has no effect upon the reaction rate. Thus, the exponent on [B] in the rate equation is 0. This allows one to conclude that the rate equation has the form of
Rate = k•[A]1•[B]0
Since any quantity raised to the 0
th power is 1, the equation can be simplified to …
Rate = k•[A]1
The rate constant k can be determined from any of the trials. Using values from trial 1, we can write
0.000230 M/min = k•(0.250 M)1
Rearranging to solve for k leads to
k = (0.000230 M/min) / (0.250 M)1
k = 0.00092 /min
The rate equation is
Rate = (0.00092 /min)•[A]1
Example 2
The method of initial rates is used to acquire the following data set for the reaction
A + B → Products.
- Determine the exponents on [A] and [B] in the rate equation.
- Determine the rate constant.
- Determine the rate equation.
- Predict the reaction rate for [A] = 0.277 M and [B] = 0.215 M.
Solution
An inspection of trials 1 and 2 shows that a doubling of [A] has no effect upon the reaction rate. Thus, the exponent on [A] in the rate equation is 0. An inspection of trials 2 and 3 shows that a doubling of [B] causes a quadrupling of the reaction rate. Thus, the exponent on [B] in the rate equation is 2. This allows one to conclude that the rate equation has the form of
Rate = k•[A]0•[B]2
Since any quantity raised to the 0
th power is 1, the equation can be simplified to …
Rate = k•[B]2
The rate constant k can be determined from any of the trials. Using values from trial 1, we can write
0.000140 M/min = k•(0.0500 M)2
Rearranging to solve for k leads to
k = (0.000140 M/min) / (0.0500 M)2
k = 0.056 /M/min
The rate equation is
Rate = (0.056 /M/min)•[B]2
If [A] = 0.277 M and [B] = 0.215 M, the rate can be determined by substitution of the concentrations into the rate equation.
Rate = (0.056 /M/min)•[B]2
Rate = (0.056 /M/min)•( 0.215 M)2
Rate = 0.00259 M/min
Example 3
The method of initial rates is used to acquire the following data set for the reaction
A + B → Products.
- Determine the exponents on [A] and [B] in the rate equation.
- Determine the rate constant.
- Determine the rate equation.
- Predict the reaction rate for [A] = 0.165 M and [B] = 0.229 M.
Solution
An inspection of trials 1 and 2 shows that a doubling of [A] doubles the reaction rate. Thus, the exponent on [A] in the rate equation is 1. An inspection of trials 1 and 3 shows that a doubling of [B] causes a doubling of the reaction rate. Thus, the exponent on [B] in the rate equation is 1. This allows one to conclude that the rate equation has the form of
Rate = k•[A]1•[B]1
The rate constant k can be determined from any of the trials. Using values from trial 1, we can write
0.000224 M/min = k•(0.100 M)1•(0.100 M)1
Rearranging to solve for k leads to
k = (0.000224 M/min) / [(0.100 M)1•(0.100 M)1]
k = 0.024 /M/min
The rate equation is
Rate = (0.024 /M/min)•[A]1•[B]1
If [A] = 0.165 M and [B] = 0.229 M, the rate can be determined by substitution of the concentrations into the rate equation.
Rate = (0.024 /M/min)•[A]1•[B]1
Rate = (0.024 /M/min)•( 0.165 M)1•( 0.229 M)1
Rate = 0.000907 M/min
Order of Reaction
The exponent on the concentrations in a rate equation are referred to as the
reaction order. If the exponent on [A] is 1, we say that the reaction is first order with respect to reactant A. If the exponent on [A] is 2, we say that the reaction is second order with respect to reactant A. And if the exponent on [A] is 0, we say that the reaction is zeroth order with respect to reactant A. Reactant B would have its own individual order and the same concepts apply to it.
So far, we have discussed differential rate equations. There is also an
integrated rate equation that expresses the concentration of a reactant as a function of time. The derivation of integrated rate equations involves calculus and is beyond the scope of this Tutorial. But the equations themselves are relevant to our discussion.
As reactants participate in reactions, their concentrations change. An integrated rate equation provides a means of predicting the concentration (
[A]) at a particular time (
t) if the initial concentration (
[A]initial) and the rate constant (
k) are known. The integrated rate equation for a 0
th, 1
st, and 2
nd order reaction varies. The generic equations for reactant A are shown in the table.
Each integrated rate equation provides a means of calculating the concentration of a reactant ([A]) at a time of t.
Next Up
You might be curious as to why some reactions are 0
th order, others are 1
st order, and still others are 2
nd order with respect to a reactant. What determines the reaction orders? What is the chemistry behind these rate equations? In
the next part of Lesson 1, we will dip our toes into the shallow waters of a very deep topic - reaction mechanisms. Our hope is to get a glimpse into the fascinating answers to these questions. But before you click ahead, take some time to ensure your understanding by using one or more of the suggestions in the
Before You Leave section.
Before You Leave
- Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Kinetics and Equilibrium page. There are several problem sets pertaining to reaction rates. We particularly like Rate Law Equations 3 and Rate Law Equations 4 as a follow-up practice to this lesson.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
- Download our Study Card on The Method of Initial Rates. Save it to a safe location and use it as a review tool. (Coming Soon.)
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. The rate equation for a particular reaction shows that the rate is first order with respect to reactant A.
- If the molar concentration of A is doubled, then the rate will increase by a factor of _____.
- If the molar concentration of A is tripled, then the rate will increase by a factor of _____.
- If the molar concentration of A is quadrupled, then the rate will increase by a factor of _____.
2. The rate equation for a particular reaction shows that the rate is second order with respect to reactant A.
- If the molar concentration of A is doubled, then the rate will increase by a factor of _____.
- If the molar concentration of A is tripled, then the rate will increase by a factor of _____.
- If the molar concentration of A is quadrupled, then the rate will increase by a factor of _____.
3. Ken Etticks and Kate Ovreackshun are using the
Method of Initial Rates to determine the rate equation for a decomposition reaction. They measure the reaction rate shortly after measuring the concentration of reactant A. They repeat for a second concentration. Their results are …
| [A] |
Rate |
| 0.250 M |
2.00 x 10-4 M/min |
| 0.500 M |
4.00 x 10-4 M/min |
- What is the order of reaction with respect to reactant A?
- What is the form of the rate equation?
- What is the value of the rate constant?
- What are the units on the rate constant?
- Predict the rate of reaction when Molarity of A = 0.796 M.
4. Ken Etticks is using the
Method of Initial Rates to determine the rate equation for a decomposition reaction. He collects the following rate-concentration data:
|
Rate |
| 0.040 M |
1.53 x 10-3 M/min |
| 0.200 M |
3.825 x 10-2 M/min |
- What is the order of reaction with respect to reactant A?
- What is the form of the rate equation?
- What is the value of the rate constant?
- What are the units on the rate constant?
- Predict the rate of reaction when Molarity of A = 0.665 M.
5. Kay Vahyue is using the
Method of Initial Rates to determine the rate equation for a reaction involving reactants X and Y. She measures the reaction rate shortly after mixing X and Y together with known concentrations and repeats several trials. Her results are …
| [X] |
[Y] |
Rate |
| 0.200 M |
0.200 M |
2.26 x 10-5 M/min |
| 0.400 M |
0.200 M |
4.52 x 10-5 M/min |
| 0.400 M |
0.400 M |
9.04 x 10-5 M/min |
- What is the order of reaction with respect to reactant X?
- What is the order of reaction with respect to reactant Y?
- What is the form of the rate equation?
- What is the value of the rate constant?
- What are the units on the rate constant?
- Predict the rate of reaction when Molarity of X = 0.568 M and Molarity of Y = 0.596 M.