Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Gas Laws
Part f: Combined Gas Law
Part a:
Pressure and Temperature
Part b:
Volume and Temperature
Part c:
Pressure and Volume
Part d:
Volume and the Number of Moles
Part e:
The Ideal Gas Law
Part f: Combined Gas Law
Part g:
Dalton's Law of Partial Pressure
Part h:
Graham's Law of Effusion
Introduction
On the first four pages of Lesson 2, several gas laws were introduced. Each gas law isolated two of the four state variables. There was a pressure-temperature gas law, a volume-temperature gas law, a pressure-volume gas law, and a volume-moles gas law. On this page, we will investigate a three-variable gas law - the Combined Gas Law.
The Combined Gas Law
Let’s suppose that we have a gas-filled container that has a pressure, temperature, and volume that can be varied. And suppose it is a sealed container such that the number of moles of gas is constant. Its state is changed from one set of pressure-temperature-volume conditions to a second set of pressure-temperature-volume conditions. How can the pressure-temperature-volume conditions of state 1 be mathematically related to the pressure-temperature-volume conditions of state 2?

This question can be answered using the ideal gas law:
P•V = n•R•T
The first step is to rearrange the equation so that all the variables (P, V, and T) are on one side and the constants (n and R) are on the opposite side. This is shown below. Since n and R are both constants, the right side of the equation can be replaced by k (k stands for constant). Then the equation can be applied to both State 1 and State 2. Both the P1•V1/T1 ratio and the P2•V2/T2 ratio are equal to the same k value. Thus, they can be set equal to one another.
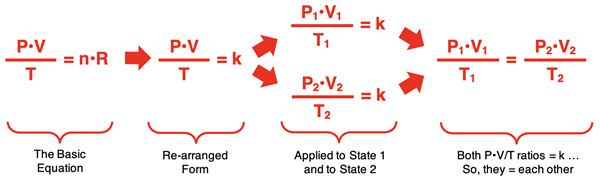
In the last step, a state equation is generated that relates the pressure, volume, and temperature in one state (P1, V1, and T1) to the pressure, volume, and temperature of a second state (P2, V2, and T2). This final equation is known as the Combined Gas Law. It applies to any sample of gas having a constant number of moles.

The combined gas law is one more gas law equation that can be used in the solution of gas law problems. Here are three examples with accompanying solutions. Additional examples are provided in the Check Your Understanding section.
Example 1
A bag is inflated to a volume of 3.89 L at 111 kPa and 23.0 °C. If the volume drops to 3.05 L at a temperature of 4.2 °C, then what is the new pressure?
Solution:
We recommend that you begin by writing down the given values, equating them with the appropriate symbol. Then identify the unknown value. Finally, substitute the numerical values into the equation and solve using proper algebra. The solution looks like this:
Given:
P1 = 111 kPa
V1 = 3.89 L
Temp1 = 23.0 °C ==> (add 273.15 for K) ==> T1 = 296.15 K
V2 = 3.05 L
Temp2 = 4.2°C ==> (add 273.15 for K) ==> T2 = 277.35 K
Unknown: P2 = ???
Equation: (P1 • V1 / T1) = (P2 • V2 / T2)
Rearrange equation to solve for P2: P2 = T2 • P1 • V1 / (T1 • V2)
Substitute values into the equation:
P2 = (277.35 K) • (111 kPa) • (3.89 L) / [ (296.15 K) • (3.05 L) ]
Use your calculator to solve: P2 = 133 kPa (rounded from 132.583406 …)
Note that the temperature values must be converted to Kelvin temperature before substituting into the equation. The pressure and volume can be any unit as long as it is the same unit in the initial and final state.
Example 2
A balloon full of Helium gas has a volume of 132 L at 99.7 kPa and 30.5 °C. What temperature is required for the balloon to have a volume of 176 L at a pressure of 77.6 kPa?
Solution:
Given:
P1 = 99.7 kPa
V1 = 132 L
Temp1 = 30.5 °C ==> (add 273.15 for K) ==> T1 = 303.65 K
P2 = 77.6 kPa
V2 = 176 L
Unknown: T2 = ???
Equation: (P1 • V1 / T1) = (P2 • V2 / T2)
Rearrange equation to solve for T2: T2 = T1 • P2 • V2 / (P1 • V1)
Substitute values into the equation:
T2 = (303.65 K) • (77.6 kPa) • (176 L) / [ (99.7 kPa) • (132 L) ]
Use your calculator to solve: T2 = 315 K (rounded from 315.121899 …)
The above answer is a Kelvin temperature. The Celsius temperature is 42.0 °C.
Example 3
Jada is in Mr. Tooker's STEM Chem class. She is experimenting with an air-filled syringe. She measures its pressure and temperature to be 1.09 atm at 28.4°C. She then places the syringe in a boiling water bath and observes the temperature and pressure to be 97.0°C and 1.23 atm. The volume of air in the syringe when in the boiling water bath is 16.2 mL. Determine the original volume.
Solution:
Given:
P1 = 1.09 atm
Temp1 = 28.4 °C ==> (add 273.15 for K) ==> T1 = 301.55 K
P2 = 1.23 atm
Temp2 = 97.0 °C ==> (add 273.15 for K) ==> T2 = 370.15 K
V2 = 16.2 mL
Unknown: V1 = ???
Equation: (P1 • V1 / T1) = (P2 • V2 / T2)
Rearrange equation to solve for V1: V1 = V2 • P2 • T1 / (P1 • T2)
Substitute values into the equation:
V1 = (16.2 mL) • (1.23 atm) • (301.55 K) / [ (1.09 atm) • (370.15 K) ]
Use your calculator to solve: V1 = 14.9 mL (rounded from 14.89276 …)
Before You Leave
- Download our Study Card on The Combined Gas Law. Save it to a safe location and use it as a review tool.
- Problem Set GL6 in our Calculator Pad section provides six awesome practice problems. Visit Problem Set GL6: Combined Gas Law.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the
Check Answer buttons when ready.
1. The combined gas law is sometimes stated as P•V/T = k where k is a proportionality constant. Use this proportionality statement to answer the following questions pertaining to a sample of gas with a constant number of moles.
- If the pressure is doubled and the Kelvin temperature is doubled, then the new volume will be _____________ the original volume. (Options: the same as, two times greater than, two times smaller than, four times greater than, four times smaller than).
- If the pressure is doubled and the Kelvin temperature is halved, then the new volume will be _____________ the original volume. (Options: the same as, two times greater than, two times smaller than, four times greater than, four times smaller than).
- If the pressure is halved and the Kelvin temperature is doubled, then the new volume will be _____________ the original volume. (Options: the same as, two times greater than, two times smaller than, four times greater than, four times smaller than).
- If the pressure is tripled and the Kelvin temperature is doubled, then the new volume will be _____________ the original volume. (Options: six times greater than, six times smaller than, 1.5 times greater than, 1.5 times smaller than).
- If the pressure is doubled and the Kelvin temperature is tripled, then the new volume will be _____________ the original volume. (Options: six times greater than, six times smaller than, 1.5 times greater than, 1.5 times smaller than).
- If the pressure is tripled and the Kelvin temperature is halved, then the new volume will be _____________ the original volume. (Options: six times greater than, six times smaller than, 1.5 times greater than, 1.5 times smaller than).
- If the pressure is halved and the Kelvin temperature is tripled, then the new volume will be _____________ the original volume. (Options: six times greater than, six times smaller than, 1.5 times greater than, 1.5 times smaller than).
2. Which change would cause the volume of a gas sample to increase? Select all that apply.
- Increase the pressure of the gas.
- Decrease the pressure of the gas.
- Increase the Kelvin temperature of the gas.
- Decrease the Kelvin temperature of the gas.
3. Starting with the state equation P
1•V
1/T
1 = P
2•V
2/T
2, use algebra to write it in six different algebraic forms. Generate a V
1 =, a V
2 =, a P
1 =, a P
2 =, a T
1 =, and a T
2 = equation.
4. A 3.55-liter sample of nitrogen gas at 24.0°C and 745mm Hg is heated to a new temperature of 121.1°C. As a result, the pressure changes to 772 mm Hg. Determine the new volume of the gas sample.
5. A sample of gas occupies a volume of 28.3 mL at STP conditions. The entire contents are transferred to a 15.5 mL container at a temperature of 44.6°C. What is the new pressure (in psi) of the gas?