Lesson 2: Gas Laws

Part h: Graham's Law of Effusion

Diffusion vs. Effusion

There are two often-confused processes that involve the movement of gas particles. They are diffusion and effusion. Diffusion is a process in which gas particles (or liquid particles) move from an area of high concentration to an area of low concentration. If your Chemistry teacher opens a bottom of ammonia on the front lab table, the particles of ammonia will begin to diffuse throughout the room. Ammonia particles move from the point of highest concentration - at the bottle opening - to the distant corners of the room where there would be close to zero concentration. The rate at which this diffusion process occurs is dependent upon the temperature of the room, the size of the particles, and the difference in concentration between the two locations. Higher temperatures, smaller molecules, and large concentration differences lend themselves to higher rates of diffusion. Diffusion generally happens very slowly since the diffusing particles undergo frequent collisions with the particles that already occupy the volume of the container.
 
Effusion is a different process. Effusion refers to the movement of particles through a small hole or opening in its container and into the surrounding space. The gradual deflation of a balloon is an example of effusion. The balloon deflates because gas particles in the balloon pass through pinholes or pores in the balloon’s surface. The rate at which a gas diffuses is dependent upon the molar mass of the gas. Less massive gases effuse at higher rates. Unlike diffusion, effusion seems to follow simpler rate laws. Quantitative comparisons of effusion rates for different gases is rather straightforward.

Graham’s Law

The rates at which gases effuse through an opening varies inversely with their molar mass. In comparing Gas A to Gas B, it can be stated that the ratio of their effusion rates is inversely proportional to the square root of ratio of their molar masses. In equation form, it can be stated that …

 
where R represents the effusion rate and MM represents the molar mass. This law is known as Graham’s Law, named in honor of Scottish chemist Thomas Graham who is credited with its discovery.
 
Let’s say that we use Graham’s Law to compare the effusion rates of helium gas and methane (CH₄) gas. Their molar mass values are 4.0 g/mol and 16.0 g/mol, respectively. Methane gas particles are four times more massive than helium gas particles. Which would effuse at a higher rate and by what factor? Since helium is lighter, it will effuse at a higher rate. Helium is four times lighter; since  √4.0 is 2.0, the effusion rate of helium gas is two times greater than methane gas.

 
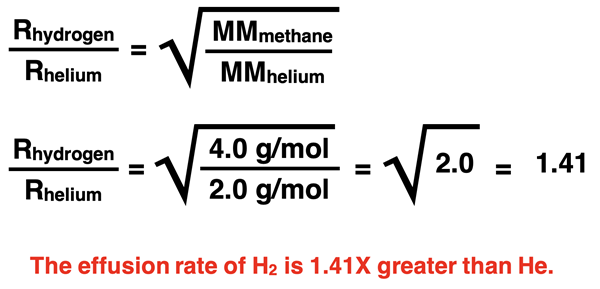
Now let’s compare helium gas and hydrogen (H₂) gas. Their molar mass values are 4.0 g/mol and 2.0 g/mol, respectively. Helium particles are twice as massive as hydrogen particles so hydrogen will effuse at a higher rate. The ratio of their molar masses is 2.0 and √2.0 is 1.41. Hydrogen’s effusion rate will be 1.41 times greater than helium’s effusion rate.

Example 1

Compare the effusion rates of oxygen (O₂) gas and methane (CH₄) gas. Which would effuse at a higher rate and by what factor?
 

Solution:

The molar mass values of methane and oxygen are 16.0 g/mol and 32.0 g/mol, respectively. Oxygen particles are twice as massive as methane particles so methane will effuse at a higher rate. The ratio of their molar masses is 2.0 and √2.0 is 1.41. Methane’s effusion rate will be 1.41 times greater than oxygen’s effusion rate
 

Example 2

Gas X is observed to effuse from a container at a rate that is 3.29 times greater than the effusion rate of Gas Y. Which gas has the greatest molar mass? And how many times greater is its molar mass?
 

Solution:

This is an example in which the solution will proceed backwards from knowledge of the ratio of effusion rates to the ratio of molar masses. The gas that has the lowest effusion rate is the most massive. So, Gas Y is the more massive of the two gases. The 3.29 is the ratio of the effusion rate; it is the square root of the molar mass ratio. So, the molar mass ratio is 3.29² or 10.82. From this calculation, we conclude that Gas Y has a molar mass that is 10.82 times greater than the molar mass of Gas X.

Effusion Rates Versus Speed

Effusion rates are most often expressed as the amount of gas (usually in moles) per unit of time. A typical unit would be moles per hour (mol/hr). Notice that this is not a speed unit and it doesn’t describe how fast a gas moves. A speed unit like mile/hour or meter/second is a distance traveled per time. Effusion rates are an amount of gas passing through an opening per second. There is no distance involved in an effusion rate measurement.
 
It ends up that the equation describing the ratio of effusion rates looks nearly identical to the equation comparing the ratio of the average speeds of gas particles. Two different gases at the same temperature will be moving about their container with an average speed that is inversely proportional to the square root of their molar mass values. Despite the similarity between the two ratios, it is important to remember that Graham’s law is comparing effusion rates. We will return to the concept of average particle speed in Lesson 4.
 
 
 

Example 3

Two identical balloons held at the same temperature and pressure are filled with two different gases. Balloon A is filled with helium gas. It takes 36 hours before the gas effuses from the balloon. Balloon B is filled with nitrogen (N₂) gas. Estimate the time that it would take for the nitrogen to effuse from the Balloon B.
 

Solution:

The molar masses of helium and nitrogen gas are 4.0 g/mol and 28.0 g/mol respectively. The helium is lighter by a factor of 7. Helium would effuse at a rate that is √7 or 2.65 times faster than nitrogen. Because of its higher effusion rate, it will take less time for the helium balloon to empty. In fact, it should take 2.65 times more time for the nitrogen balloon to empty. Therefore, Balloon B will be empty in 95 hours.

36 hours • √7 = 95.247047 … hours

Before You Leave

• Download our Study Card on Graham’s Law. Save it to a safe location and use it as a review tool. (Coming Soon.)
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

Check Your Understanding

1. Rank the balloons from lowest to highest effusion rates. 
   
   Check Answer
   Answer: B < D < C < A (B is lowest and A is highest)
   
   Do a quick and dirty molar mass calculation. (A: 20 g/mol; B: 71 g/mol; C: 32 g/mol; and D: 44 g/mol) Then list the gas with the largest molar mass first and the smallest molar mass last.
   
    
   
    
2. Rank the balloons from lowest time to highest time for the gas to empty by effusion. 
   
   Check Answer
   Answer: A < C < D < B (A is lowest and D is highest)
   
   Do a quick and dirty molar mass calculation. (A: 20 g/mol; B: 71 g/mol; C: 32 g/mol; and D: 44 g/mol) Then list the gas with the smallest molar mass first; it is lightest and effuses at the highest rate and will empty from the balloon in the least time. List the gas with the highest molar mass last since it will take the most time to empty  from the balloon by effusion.
   
    
   
    

 
 
2. Compare Balloon C and Balloon D above. Which balloon has the greatest effusion rate and how many times is it than the other balloon?