Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Gas Laws
Part b: Volume and Temperature
Part a:
Pressure and Temperature
Part b: Volume and Temperature
Part c:
Pressure and Volume
Part d:
Volume and the Number of Moles
Part e:
The Ideal Gas Law
Part f:
Combined Gas Law
Part g:
Dalton's Law of Partial Pressure
Part h:
Graham's Law of Effusion
The Experiment
 The previous part of Lesson 2 addressed the pressure-temperature relationship. The discussion began with an experiment. On this page, we will look at the volume-temperature relationship and also begin with an experiment. This experiment involves a small air-filled balloon, a thermometer, and a large beaker. The beaker is partly filled with chilled water. The water level is marked on the beaker’s side with a marker. The balloon is completely submerged in the water and allowed time to reach the temperature of the water. The new water level is marked and the temperature recorded. The rise in water level is due to the balloon’s volume. The balloon is removed from the beaker. Water from a graduated cylinder is added to the beaker to raise the water level from the lowest to the highest mark, thus determining the balloon’s volume. The process is repeated for several water samples of varying temperatures from just above 0°C up to 85°C. The balloon is sealed so that the number of moles remains constant from trial to trial. Given that the balloon is flexible, the internal pressure adjusts to match the external pressure; this is constant from trial to trial. Sample data and a graph for this experiment is shown below.
The previous part of Lesson 2 addressed the pressure-temperature relationship. The discussion began with an experiment. On this page, we will look at the volume-temperature relationship and also begin with an experiment. This experiment involves a small air-filled balloon, a thermometer, and a large beaker. The beaker is partly filled with chilled water. The water level is marked on the beaker’s side with a marker. The balloon is completely submerged in the water and allowed time to reach the temperature of the water. The new water level is marked and the temperature recorded. The rise in water level is due to the balloon’s volume. The balloon is removed from the beaker. Water from a graduated cylinder is added to the beaker to raise the water level from the lowest to the highest mark, thus determining the balloon’s volume. The process is repeated for several water samples of varying temperatures from just above 0°C up to 85°C. The balloon is sealed so that the number of moles remains constant from trial to trial. Given that the balloon is flexible, the internal pressure adjusts to match the external pressure; this is constant from trial to trial. Sample data and a graph for this experiment is shown below.
Image Source: Pasco
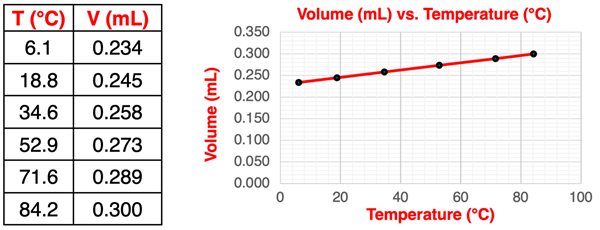
A Deeper Look at the Data
The graph shows a linear relationship between volume and temperature. Let’s postpone writing an equation and do a deeper analysis. Let’s extend the line on the graph leftward until it intersects with the x-axis. At what temperature does the volume drop to 0? The result is shown below.
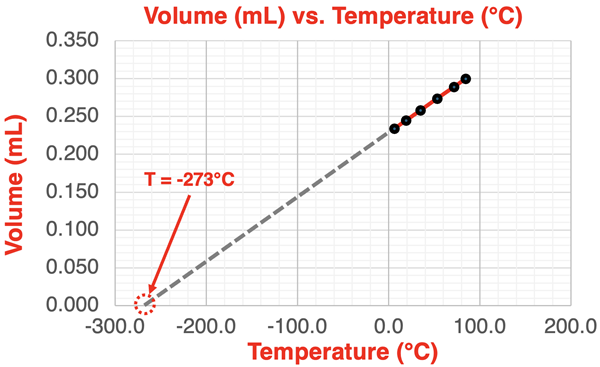
The temperature at which the volume drops to 0 mL is approximately -273°C. Do you recognize that number? That is a temperature of 0 on the Kelvin temperature scale. This temperature is referred to as absolute zero … the lowest temperature theoretically achievable. A gas has no volume at 0 K.
Now let’s change the plot to a Volume vs. Kelvin Temperature plot.
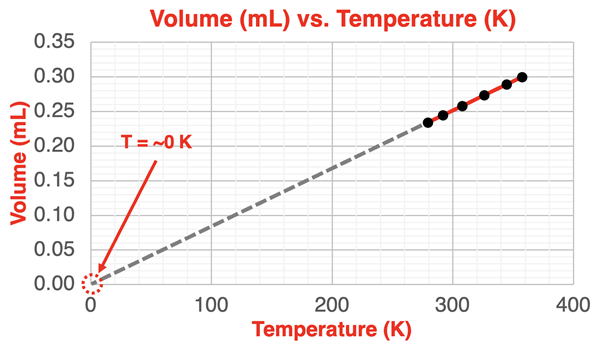
When plotting Kelvin temperature along the x-axis, we achieve a y-intercept of 0 mL. The slope-intercept equation (y = mx + b) can be used to write an equation that describes the collected data. The y-intercept drops out of the equation.
Volume (mL) = m • Temperature (K)
where m represents the slope of the line. In the case of our experiment, the slope is 0.000839 mL/K. Experiments of this nature have been repeated numerous times and the results confirm the conclusion that the volume of a gas is directly proportional to its Kelvin temperature.
Charles’ Law
This experiment leads us to another gas law. It is referred to as Charles’ Law, in honor of French scientist, mathematician, and balloonist Jacques Charles who is credited with its discovery. The law can be stated as follows:
For a sample of gas with a constant pressure and number of moles, the volume of the gas is directly proportional its Kelvin temperature.
This proportionality statement is often written in equation form as
V = k•T
where V is the volume, T is the Kelvin temperature, and k is a proportionality constant.
 The idea of a directly proportional relationship indicates that the factor by which the Kelvin temperature is changed is the same factor by which the volume changes. The sample data at the right illustrate this relationship. A doubling of the Kelvin temperature causes a doubling of the volume. We see this pattern in Rows 1 and 2. The temperature is doubled from 50 K to 100 K and the volume is doubled as a result, from 60 mL to 120 mL. Similarly, a tripling of the Kelvin temperature causes a tripling of the volume. This is observed in Rows 1 and 3. The temperature is tripled from 50 K to 150 K and the volume is tripled as a result, from 60 mL to 180 mL. Finally, a quadrupling of the Kelvin temperature causes a quadrupling of the volume. We see this pattern in Rows 1 and 4. The temperature is quadrupled from 50 K to 200 K and the volume is quadrupled from 60 mL to 240 mL.
The idea of a directly proportional relationship indicates that the factor by which the Kelvin temperature is changed is the same factor by which the volume changes. The sample data at the right illustrate this relationship. A doubling of the Kelvin temperature causes a doubling of the volume. We see this pattern in Rows 1 and 2. The temperature is doubled from 50 K to 100 K and the volume is doubled as a result, from 60 mL to 120 mL. Similarly, a tripling of the Kelvin temperature causes a tripling of the volume. This is observed in Rows 1 and 3. The temperature is tripled from 50 K to 150 K and the volume is tripled as a result, from 60 mL to 180 mL. Finally, a quadrupling of the Kelvin temperature causes a quadrupling of the volume. We see this pattern in Rows 1 and 4. The temperature is quadrupled from 50 K to 200 K and the volume is quadrupled from 60 mL to 240 mL.
The State Equation
We have emphasized in this chapter that there are four variables - pressure, temperature, volume, and the number of moles - that describe a sample of a gas. The values of these variables will often change. In the experiment discussed above, the volume and temperature change in direct proportion to one another. We might say that the gas sample changes from one state with a set of P-T-V-n conditions to another state with a different set of a set of P-T-V-n conditions. This is what we call a state change.
The equation V = k•T describes the direct proportionality between the two quantities. But it is often more useful to express the relationship as a state equation. A state equation relates the variable values at one state to the variable values for another state after a change has occurred. Through a collection of sequential and logical steps, the V = k•T equation can be converted to a state equation. This is shown below:
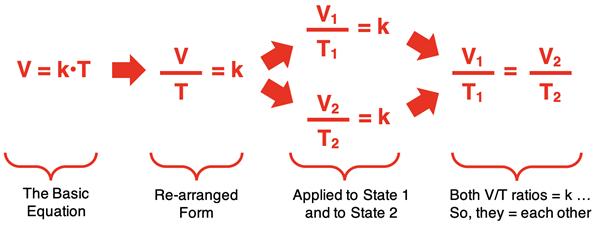
In the last step, a state equation is generated that relates the volume and temperature in one state (V1 and T1) to the volume and temperature of a second state (V2 and T2). This is one of the forms in which Charles’ law is commonly stated.

This state equation is often used in the solution of gas law problems. Here are two examples with accompanying solutions. Additional examples are provided in the Check Your Understanding section.
Example 1
Bert Day is having a party and his parents visit the Party Store and purchase a large helium balloon. Inside the store, the balloon has a volume of 17.4 L and a temperature of 33.4°C. Once taken outside, the temperature of the helium quickly decreases to 3.6°C. What will be the new volume of the balloon?
Solution:
We recommend that you begin by writing down the given values, equating them with the appropriate symbol. Then identify the unknown value. Finally, substitute the numerical values into the equation and solve using proper algebra. The solution looks like this:
Given:
V1 = 17.4 L
Temp1 = 33.4°C ==> Add 273.15 ==> T1 = 306.55 K
Temp2 = 3.6°C ==> Add 273.15 ==> T2 = 276.75 K
Unknown: V2 = ???
Equation: (V1 / T1) = (V2 / T2)
Rearrange equation to solve for V2: V2 = T2 • V1 / T1
Substitute values into the equation: V2 = (276.75 K) • (17.4 L) / (306.55 K)
Use your calculator to solve: V2 = 15.7 L (rounded from 15.7085 …)
Note that the temperature values must be converted to Kelvin temperature before substituting into the equation. The volume can be any volume unit.
Example 2
A gas sample with a volume of 3.90 L at a temperature of 30.6°C is heated until its new volume is 6.51 L. Assuming a constant pressure, what is the new temperature (in °C) of this sample of gas?
Solution:
We will use the same approach as before, organizing our given information, identifying the unknown, and substituting and solving with good algebra. We will once again be certain to use the equation with Kelvin temperature values.
Given:
V1 = 3.90 L
V2 = 6.51 L
Temp1 = 30.6°C ==> Add 273.15 ==> T1 = 303.75 K
Unknown: Temp2 = ???
Equation: (V1 / T1) = (V2 / T2)
Rearrange equation to solve for T2: T2 = T1 • V2 / V1 (requires a few algebra steps)
Substitute values into the equation: T2 = (303.75 K) • (6.51 L) / (3.90 L)
Use your calculator to solve: T2 = 507.0288 … K
Now convert to °C:
Temp2 = 507.0288 … K - 273.15 K
Temp2 = 233.9 °C (rounded from 233.8788 …)
Conclusion
We have now discussed two gas laws - one for pressure and temperature and one for volume and temperature. Historically, both laws have a strong empirical basis. And in most Chemistry courses, the introduction of the law begins with an experiment. We will take the same approach as we continue our discussion of gas laws. Next up is the pressure-volume gas law. But before you move onward, please check out our learning suggestions below.
Before You Leave
- Download our Study Card on Volume and Temperature. Save it to a safe location and use it as a review tool.
- Try our Volume and Temperature Concept Builder. It coordinates well with this lesson and provides exceptional practice.
- Problem Set GL4 in our Calculator Pad section provides six awesome practice problems. Visit Volume and Temperature.
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the
Check Answer buttons when ready.
1.
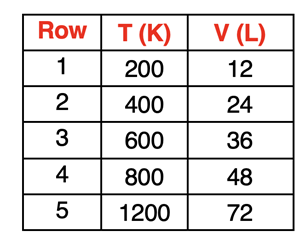
Consider the table at the right in answering the questions.
- Identify at least two sets of two rows that illustrate that a doubling of the Kelvin temperature will double the volume.
- Complete the sentence: Rows 1 and 4 illustrate that increasing the Kelvin temperature by a factor of ______ will cause the volume to __________ (increase, decrease) by a factor of _____.
- Predict the value of the volume when the Kelvin temperature is 1000 K.
- Predict the value of the volume when the Kelvin temperature is 1600 K.
- Predict the value of the volume when the Kelvin temperature is 500 K.
2. Which change would cause the volume of a gas sample to increase?
- Increase the temperature of the gas.
- Decrease the temperature of the gas.
3. Starting with the state equation V
1/T
1 =V
2/T
2, use algebra to write it in four different algebraic forms. Generate a V
1 =, a V
2 =, a T
1 =, and a T
2 = equation.
4. A hot air balloon has a volume of 3125 liters at 40.0°C. What temperature would be required to give it a volume of 3952 liters?
5. Gas in a balloon occupies 123 mL at -12.0°C. What will be its volume at a temperature of 86.5°C?