Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Gas Laws
Part d: Volume and the Number of Moles
Part a: Pressure and Temperature
Part b: Volume and Temperature
Part c: Pressure and Volume
Part d: Volume and the Number of Moles
Part e: The Ideal Gas Law
Part f: Combined Gas Law
Part g: Dalton's Law of Partial Pressure
Part h: Graham's Law of Effusion
A Thought Experiment
On the first three pages of Lesson 2, we have explored three different gas laws – the laws pertaining to pressure and temperature, to volume and temperature, and to pressure and volume. Each page began with the discussion of an experiment that is often performed in a first year Chemistry course. On this page we will explore the relationship between the number of moles of gas and the volume. But we will be breaking the pattern of beginning with an actual experiment performed in a Chemistry course. The task of measuring the moles of gas requires a mass measurement. Most high schools do not have equipment capable of acquiring an accurate measurement of a small sample of gas. So, our approach will be to present a thought experiment.
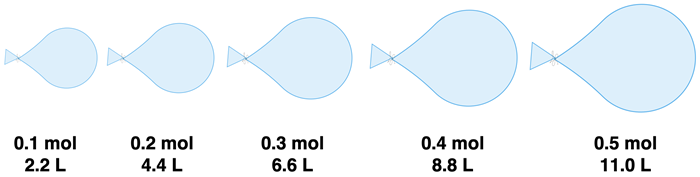
Suppose that you have a collection of identical balloons. And suppose that you have calibrated your lungs to inhale and then accurately exhale 0.10 mol of gas on each inhale-exhale cycle. And you decide to exhale different number of moles of gas into the different balloons, tie them, and determine their volume by water displacement. In each case, the temperature is a constant value (you allow the balloons to establish a room temperature before measuring volume). And because of the flexibility of the balloons, they each expand to the point that the gas pressure equals the room pressure. Each balloon will have the same temperature and pressure. What would you find out from such an experiment? The graphic below displays one of the likely findings. For every 0.10 mol of gas added to the balloon, its volume increases by a constant amount of 2.2 L.
Avogadro’s Law
The data from this thought experiment illustrate the volume-mole relationship. It can be stated like this:
For a sample of gas held at a constant pressure and temperature, the volume of the gas is directly proportional to the number of moles of gas.
This law is often referred to as Avogadro’s Law in honor of Italian scientist Amedeo Avogadro who is credited with its discovery. The proportionality statement is often written in equation form as
V = k•n
where V is the volume, n is the number of moles, and k is a proportionality constant.
The idea of a directly proportional relationship indicates that the factor by which the number of moles is changed is the same factor by which the volume changes. The sample data at the right illustrate this relationship. A doubling of the number of moles causes a doubling of the volume. We see this pattern in Rows 1 and 2. The number of moles is doubled from 1 mol to 2 mol and the volume is doubled as a result, from 22 L to 44 L. Similarly, a tripling of the number of moles causes a tripling of the volume. This is observed in Rows 1 and 3. The number of moles is tripled from 1 mol to 3 mol and the volume is tripled as a result, from 22 L to 66 L. Finally, a quadrupling of the number of moles causes a quadrupling of the volume. We see this pattern in Rows 1 and 4. The number of moles is quadrupled from 1 mol to 4 mol and the volume is quadrupled from 22 L to 88 L.
The State Equation
We have been emphasizing the interdependence of the four state variables throughout this chapter. The four state variables that describe every sample of a gas are pressure, temperature, volume, and the number of moles. The values of these variables often change. In the thought experiment discussed above, the volume and number of moles changed in direct proportion to one another. We might say that the gas sample experienced a change of state. It changed from one state with a set of P-T-V-n conditions to another state with a different set of a set of P-T-V-n conditions.
The equation V = k•n describes the direct proportionality between the two quantities. But it is often more useful to express the relationship as a state equation. A state equation relates the variable values at one state to the variable values for another state after a change has occurred. Through a collection of sequential and logical steps, the V = k•n equation can be converted to a state equation. This is shown below:
In the last step, a state equation is generated that relates the volume and number of moles in one state (V1 and n1) to the volume and number of moles of a second state (V2 and n2). This is one of the forms in which Avogadro’s law is commonly stated.
This state equation is often used in the solution of gas law problems. Here is an example with an accompanying solution. One additional example is provided in the Check Your Understanding section.
Example:
A balloon is inflated with 0.0372 moles of gas. Before tying the balloon, its volume is measured to be 0.841 L. Then 0.0215 moles of gas are emptied from the balloon and it is tied off. What is the new volume of the balloon?
Solution:
We recommend that you begin by writing down the given values, equating them with the appropriate symbol. Then identify the unknown value. Finally, substitute the numerical values into the equation and solve using proper algebra. The solution looks like this:
Given:
n1 = 0.0372 mol
V1 = 0.841 L
n2 = 0.0157 mol
(The n2 value is found by subtraction: 0.0372 mol - 0.0215 mol)
Unknown: V2 = ???
Equation: (V1 / n1) = (V2 / n2)
Rearrange equation to solve for V2: V2 = n2 • V1 / n1
Substitute values into the equation: V2 = (0.0157 mol) • (0.841 L) / (0.0372 mol)
Use your calculator to solve: V2 = 0.355 L (rounded from 0.3549381 …)
Molar Volume
Avogadro’s law is stated in a variety of ways. The more common form of the law is …
At the same pressure and temperature, equal volumes of different gases have the same number of moles.
Imagine filling identical balloons to the same volume with different gases. In the same room, the balloons would have the same pressure and temperature. And because they do, they would also contain the same number of moles of each gas. For instance, suppose the balloons each contained 0.010 moles of different gases. They would each have the same volume. The actual volume would be dependent upon the temperature and pressure of the room (and thus, of the gases inside the balloon). A typical volume might be 2.24 L for each balloon.
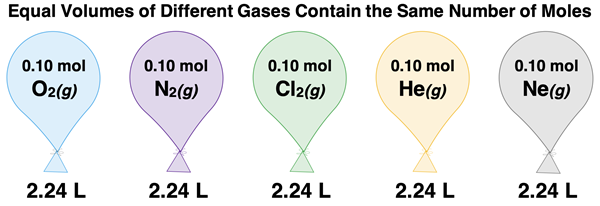
The ratio of the volume to number of moles is the same for the five different gases. We could represent this principle mathematically as …
The ratio of volume to the number of moles is known as the molar volume of the gas. The definition of molar volume is similar to the definition of molar mass. The molar mass is defined as the mass per 1 mole of a substance. The molar volume is defined as the volume of 1 mole of a substance.
Avogadro’s Law would suggest that for different gases, the molar volume would be the same value for the same pressure and temperature. As mentioned above, the actual volume-per-mole ratio is dependent upon the actual values of pressure and temperature. There is one particular pressure and temperature that has been designated as a standard for comparing gas samples. We refer to it as Standard Temperature and Pressure, affectionately remembered as STP. STP conditions include a Temperature of 0°C (or 273.15 K) and a Pressure of 1.00 atm (101.325 kPa or 760 mmHg). At STP conditions, 1.00 mole of any gas would occupy a volume of 22.4 liter.
Conclusion
Lesson 2 of Chapter 10 of our Chemistry Tutorial is focused on gas laws -patterns of behavior that describe how changes in one variable affect another variable. We now have discussed four different gas laws:
Next up is what many would call the most important gas law of them all - the ideal gas law. But before you move forward, please check out our learning suggestions below to make sure you have a firm understanding of the volume-mole relationship.
Before You Leave
- Download our Study Card on Volume and the Number of Moles. Save it to a safe location and use it as a review tool. (Coming Soon.)
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
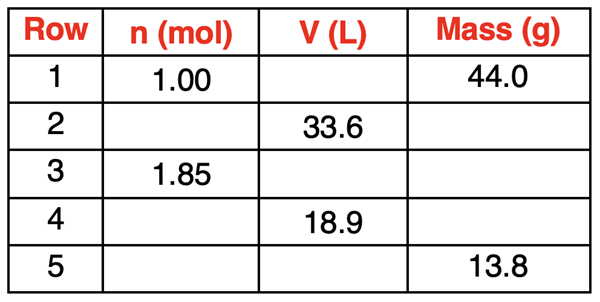
1. Consider the table at the right in answering the questions.
- Identify at least two sets of two rows that illustrate that a doubling of the number of moles will double the volume.
- Complete the sentence: Rows 1 and 4 illustrate that increasing the number of moles by a factor of ______ will cause the volume to __________ (increase, decrease) by a factor of _____.
- Predict the value of the volume when the number of moles is 60 mol.
- Predict the value of the volume when the number of moles is 80 mol.
- Predict the value of the volume when the number of moles is 45 mol.
2. Which change would cause the volume of a gas sample to increase?
- Increase the number of moles of the gas.
- Decrease the number of moles of the gas.
3. Starting with the state equation V1/n1 =V2/n2, use algebra to write it in four different algebraic forms. Generate a V1 =, a V2 =, a n1 =, and a n2 = equation.
4. A teacher adds 0.0232 moles of a gas into a balloon. The volume is 525 mL. If the teacher adds another 0.0356 moles of gas, then what will be its new volume?
5. “STP” stands for …
- Stabilized Temperature and Pressure
- Secret Temperature and Pressure
- Specialized Temperature and Pressure
- Standard Temperature and Pressure
6. What is so special about STP that is NOT true of other temperatures and pressures?
- The ratio of volume to moles is the same for all gases at STP.
- The molar mass of all gases is the same at STP.
- 1 mole of any gas has the same volume at STP.
- 1 mole of any gas has a volume of 22.4 L at STP.
7. Perform calculations to complete the following table for carbon dioxide (CO2) gas at STP conditions:
